ЧОХЩЯДЛИ, полином – Ах^кй^л…ω^м+ Бх^нй^п …ω^г+…+Дх^рй^с…ω^т шяклиндя ифадя олунан сонлу сайда бирщядлинин ъями, бурада х, й, …, ω – дяйишянляр, А, Б, Д ( ч о х щ я д л  и н и н  я м с а л л а р ы) вя к, л, т (г ц в в я т  ц с т л  я р и  мцсбят там ядядлярдир) – сабитлярдир.

                                                                                       Ах^кй^л…ω^м

шяклиндя топлананлар чохщядлинин щядляри адланыр. Щядлярин, щямчинин щяр щяддяки вуругларын йерини ихтийари гайдада дяйишмяк олар; еляъя дя ямсалы сыфыр олан щядляри, щямчинин щяр бир щяддя дяряъяси сыфыр олан вуруьу атмаг вя йа ялавя етмяк олар. Ч.-нин бир, ики вя йа цч щядди варса, о, б и р щ я д л и,  и к и щ я д  л и  вя йа   ц ч щ я д ли адланыр.

Ч.-нин ямсалына ясасян онун щансы мейдана, мяс., расионал, щягиги вя йа комплекс ядядляр мейданына аид олмасы щаггында тясяввцр йараныр.

Яэяр Ч.-нин ики щяддиндя ейни дяйишянлярин гцввят цстляри ъцт-ъцт бярабяр оларса, онда онлар охшар щядляр адланыр. Юз араларында охшар олан

                                      А′х^кй^л…ω^м, Б′х^кй ^л…ω^м, Д′х^кй^л…ω^м

щядляри ейни бир (охшар щядлярин ислащы)

                                        (А′+Б′+Д′) х^кй^л…ω^м

иля явяз етмяк олар. Охшар щядлярин ислащындан сонра ямсалы сыфырдан фяргли олан ики Ч.-нин бцтцн щядляри ъцт-ъцт бярабяр оларса (лакин мцхтялиф ардыъыллыгла да йазыла биляр), еляъя дя бу чохщядлилярин бцтцн ямсаллары сыфра бярабяр оларса, онда беля Ч.-ляр бярабяр Ч.-ляр адланыр. Сонунъу щалда дейирляр ки, Ч. ейнилик кими сыфра бярабярдир вя 0 иля ишаря едирляр. Бир х дяйишяниндян асылы олан чохщядлини щямишя

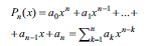
шяклиндя йазмаг олар. Бурада, а₀, а₁, …, а_н ямсаллардыр. П_н(х)=0 ъябри тянлийинин щялли щяр щансы мейданда П_н(х) чохщядлисинин кюкц адланыр. Ч.-нин кюкляри иля ямсаллары Вийет дцстуру васитясиля ялагялидир (бах Вийет теореми).

Ч.-нин щяр щансы щяддиндяки дяряъялярин ъями щямин щяддин дяряъяси адланыр. Яэяр Ч. ейнилик кими сыфыр дейился, онда, ямсалы сыфырдан фяргли олан щядляр ичярисиндя бир вя йа бир нечя ян йцксяк дяряъяйя малик щядляр вар; бу ян бюйцк дяряъя ч о х щ я д л и н и  н  д я р я ъ я  с и адланыр. Мисаллар: хйз+х+й+з цчдяряъяли, 2х+й –з+1 бирдяряъяли (хятти чохщядли) чохщядлидир, 5х² –2х² –3х² -нын дяряъяси йохдур, чцнки о, ейнилик кими сыфырдыр. Бцтцн щядляри ейни дяряъяйя малик олан Ч., б и р ъ и н с   ч о х щ я д л и вя йа ф о р м а адланыр. 1, 2, 3 дяряъяли формалар уйьун олараг х я т т и, к в а д р а т и к, к у б и к, дяйишянлярин сайына эюря (ики, цч) – б и н а р, т е р н а р адланыр (мяс., х²+й²+з² –хй–йз+хз тернар квадратик формадыр).

Йердяйишмя, груплашдырма вя пайлама ганунлары ясасында Ч. цзяриндя топлама, чыхма вя вурма ямяллярини йериня йетирмякля йенидян Ч. алыныр. Беляликля, ямсаллары верилмиш мейдандан олан бцтцн Ч.-ляр йыьыны верилмиш мейдан цзяриндя чохщядлиляр щалгасы ямяля эятирир; бу щалга сыфрын бюлянлярини сахламыр, йяни сыфра бярабяр олмайан Ч.-лярин щасили сыфыр ола билмяз.

Яэяр ейни дяйишяндян асылы олан ики П(х) вя Г(х) чохщядлиляри цчцн еля Р(х) чохщядлиси тапмаг оларса ки, П=ГР олсун, онда дейирляр ки, П Г-йя бюлцнцр; Г бюлян, Р ися гисмят адланыр. Яэяр П Г-йя бюлцнмцрся, еля Р(х) вя С(х) чохщядлиляри тапмаг олар ки, П= ГР+С алынар. Беля ки, С(х)-ын дяряъяси Г(х)-ын (н a т а м а м г и с м я т) дяряъясиндян кичикдир. Бу ямялиййатын тякрар едилмяси иля П вя Г-нцн ян бюйцк ортаг бюлянини тапмаг олар (бах Евклид алгоритми). Яэяр Ч.-ни ямсаллары верилмиш мейдандан олан ондан кичик дяряъяли Ч.-лярин щасили шяклиндя эюстярмяк мцмкцндцрся, онда бу Ч. (верилмиш мейданда) э я т и р и л  м и ш  Ч., якс щалда э я т и р и л м я й я н Ч. адланыр.

Хцсуси Ч.-ляр системи – ортогонал чохщядлиляр, йахынлашмалар нязяриййясиндя функсийаларын сыралар шяклиндя ифадя васитяси кими истифадя едилир.

Комплекс дяйишянли функсийалар нязяриййяси бахымындан Ч. – там функсийаларын ян садя синфидир. н дяряъяли Ч. эенишлянмиш комплекс ядядляр мцстявисини юзцня еля якс етдирир ки, ω=П_н(з) образынын щяр бири н сайда з₁,з₂,…, з_н прообразына малик олур.