ЧОХОБРАЗЛЫ – хцсуси нюгтяляри олмайан дцз хятт вя мцстяви анлайышларынын чохюлчцлц цмумиляшмяси. Щяр бир нюгтяси н-юлчцлц Р^н Евклид фязасынын  ачыг кцряси иля щомеоморф олан ятрафлара малик, М тоположи фязасына н-юлчцлц т о п о л о ж и  ч о  х о б р а з л ы дейилир. Адятян, фярз едирляр ки, М беля нюв сонлу вя йа щесаби сайда ятрафларла юртцлмцшдцр вя М а й р ы л а б и л я н д и р, йяни истянилян ики нюгтясинин кясишмяйян ятрафлары вар.

Щяндясядя 1,2,3 юлчцлц Ч.-йа аид мцхтялиф мисаллара раст эялинир. Дцз хятт, ачыг интервал, парабола, чевря, еллипс – бирюлчцлц Ч.-дыр. Мцстяви цзяриндяки истянилян област, мцстяви юзц, параболоид, сфера, еллипсоид, тор вя с. икиюлчцлц чохобразлыдыр. Конусун сятщи Ч. дейил, чцнки конусун щяр ики доьуранынын бирляшдийи тяпяси даиряйя щомеоморф олан ятрафа малик дейил. Ади цчюлчцлц Евклид фязасы вя орадакы щяр бир област цчюлчцлц Ч.-дыр.

Истянилян сайда юлчмяляр цчцн Ч. анлайышы щяндяся, рийази анализ, механика вя физиканын сон дяряъя мцхтялиф тялябатлары иля ялагядар рийазиййата дахил едилмишдир. Бахылан обйектляр щягиги ядядляр системи иля параметризасийа едиля билян бцтцн ситуасийаларда бу анлайыш практики олараг тятбиг олунур. Бу щалда ямяля эялян Ч.-нын нюгтяляри мцхтялиф тябиятли обйектляр – дцз хятляр, сфералар, матрисляр, механики системин вязиййятляри вя с. ола биляр. Мяс., икили мцстяви ряггасын вязиййяти онун голларынын уълары олан дюрд координатла – (х₁, й₁) вя (х₂, й₂) иля тяйин олунур. Ряггасын щяр бир вязиййятиня дюрдюлчцлц фязанын (х₁, й₁, х₂, й₂) координатлы нюгтясини уйьун гоймагла Р⁴ фязасынын тора щомеоморф олан мцяййян нюгтяляр чохлуьуну алырлар. Цчюлчцлц фязанын Н нюгтядян ибарят олан вя н сярбястлик дяряъясиня малик механики системинин вязиййяти бир чох щалларда Р³Н-дя йерляшян н юлчцлц Ч. иля тясвир олунур.

Ч. компактдырса, она г а п а л ы Ч. дейилир, якс щалда а ч ы г Ч. адланыр. Юлчцсц 1 олан щяр бир г а п а л ы Ч. чевря иля, щяр бир а ч ы г Ч. ися дцз хятля щомеоморфдур (шякил 1-дя бирюлчцлц Ч.-лар вя П нюгтясинин онларын щяр бириндя олан ятрафы тясвир олунмушдур). Икиюлчцлц щал цчцн гапалы Ч. артыг P кифайят гядяр мцхтялиф олур. Онлар сонсуз P сайда тоположи типя айрылыр: сфера – сыфырынъы нюв сятщ (шякил 2, а), тор – биринъи нюв сятщ  (шякил 2, б), “крендел” – 2-ъи нюв сятщ (шякил 2, ъ), цмумиййятля “н голлу кцря” – н-ъи нюв сятщ (шякил 2, ч-дя н=3 олан беля сятщ тясвир едилмишдир). Бу мисалларла истигамятляндирилмямиш икиюлчцлц гапалы Ч.-нын бцтцн тоположи типляри тамамланыр. Сонсуз сайда истигамятляндирилмямиш икиюлчцлц гапалы Ч.-лар – бирцзлц сятщляр, мяс., бирцзлц тор адланан пройектив мцстяви вя щямчинин ачыг икиюлчцлц Ч.-ларын тяснифаты да мювъуддур. Цчюлчцлц Ч.-ларын там тяснифаты тапылмамышдыр (щятта гапалы Ч.-лар цчцн).

Тоположи Ч.-нын тяйини рийази анализин диференсиалланан функсийа вя диэяр анлайышларыны Ч. цзяриндя тяйин етмяйя имкан вермир. Бу анлайышларын мяна кясб етмяси цчцн Ч.-йа ялавя структурлар дахил етмяк зяруридир. н юлчцлц тоположи Ч.-нын истянилян нюгтясинин ятрафында бу нюгтянин щямин ятрафда вязиййятини биргиймятли тяйин едян локал х₁,…, х_н координатлары мювъуддур. Ч.-нын истянилян нюгтясинин ятрафында локал координатлары еля сечсяк ки, ики мцхтялиф локал координат системи кясишян ятрафларда бир-бири иля Ъ^к, к≥1 синфинин функсийалары васитясиля ифадя олунсун, онда к синфинин щамар структуруну аларыг. Адятян, к=∞ эютцрцлцр вя щамар структура малик Ч. д и ф е р е н с и а л л а н а н (вя йа щ а м а р) Ч. адландырылыр. Диференсиалланан Ч.-нын мцасир рийазиййатда бюйцк ящямиййяти вар, беля ки, мящз бу Ч.-лар тятбиг сащяляриндя эениш истифадя олунур. Ейни бир тоположи Ч.-да мцхтялиф ъцр (щятта изоморф олмайан) щамар структурлар ола биляр. Аналожи олараг аналитик Ч. анлайышы дахил едилир. Яэяр локал координатлары комплекс ядядляр щесаб етсяк вя онларын бир-бири иля аналитик функсийа васитясиля ифадя олунмасыны тяляб етсяк, онда к о м п л е к с (а н а л и т и к) чохобразлы анлайышыны аларыг.

Чохюлчцлц Ч. анлайышыны илк дяфя Б.Риман юзцнцн “Щяндясянин ясасыны тяшкил едян щипотезляр щаггында” мцщазирясиндя формуля етмишдир (1854). 1913 илдя Э.Вейл Риман сятщини, йяни бирюлчцлц комплекс чохобразлы анлайышыны (абстракт) дахил етди (комплекс дяйишянли щяр бир аналитик функсийа бу функсийанын Риман сятщи адланан Ч. васитясиля ялагяляндирилир).

Мцасир рийазиййатда Ч. анлайышынын мцхтялиф цмумиляшмяляриня дя бахылыр. Мяс., сярщядли Ч. (сяъиййяви мисал – Рн фязасында гапалы кцряси) вя щямчинин аналитик фяза (хцсуси нюгтяляря малик щягиги вя йа комплекс аналитик сятщляр дахил олан) беляляриндяндир.

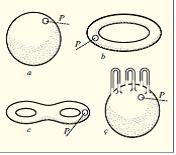    Шякил 2. Гапалы икиюлчцлц чохобразлыйа аид мисаллар.  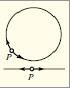                Шякил 1. Бирюлчцлц чохобразлылар.