ЧЕБЫШЕВ БЯРАБЯРСИЗЛИЙИ – 1) монотон ядяди ардыъыллыглар вя функсийалар цчцн бярабярсизлик. а1≤ а2≤… ≤ ан вя б1≤ б2≤…≤ бн вя йа а1 ≥ а2 ≥ …≥ ан вя б1≥б2≥…≥бн (ан ≥ 0, бн ≥ 0) сонлу ардыъыллыглары цчцн Ч.б.

шяклиндядир. Ч.б.-нин интеграл шякли ашаьыдакы кимидир:

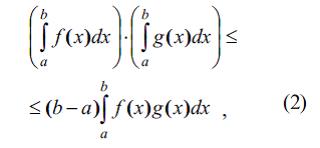
бурада ф(х) ≥ 0, э(х) ≥ 0 вя щяр ики функсийа йа азаландыр, йа да артандыр. Яэяр бир ардыъыллыг (функсийа) артырса, диэяр ардыъыллыг (функсийа) ися азалырса, онда (1) вя (2) бярабярсизликляринин ишаряляри яксиня дяйишир. Бярабярсизликляр П.Л. Чебышев тяряфиндян верилмишдир (1882). 2) Ч.б., Бйенеме–Чебышев бярабярсизлийи – тясадцфи кямиййятин онун рийази эюзлямясиндян йайынма ещтималы цчцн йухары сярщяди тяйин едян бярабярсизлик. Тутаг ки, Х – рийази эюзлямяси ЕХ=а вя дисперсийасы ДХ =σ2 олан тясадцфи кямиййятдир. Ч.б. ашаьыдакындан ибарятдир: истянилян ε > 0 цчцн 

׀Х– а׀≥ε

щадисясинин ещтималы σ2/ε2-ны ашмыр вя йа

P {│Х– а│≥ tσ} ≤ 1/t2

Бу бярабярсизлийи Ж. Бйенеме (1853) вя П.Л. Чебышев (1867) бир-бириндян асылы олмадан ашкар етмишляр. Мцасир ядябиййатда ону чох вахт Ч.б. дландырырлар. Ола биляр ки, бу, П.Л. Чебышевин бюйцк ядядляр ганунунун цмумиляшмясинин исбаты заманы бу бярабярсизликдян истифадя етмяси иля ялагядар олмушдур. Бязи ялавя фярзиййялярля Ч.б.-нин дягиглийи артырыла биляр: 1/t2 дяряъя гиймятляндирмяси т-нин артмасы иля бюйцк сцрятля азалан ямсаллы гиймятляндирмя иля явяз олуна биляр. Ч.б. вя онун бцтцн мцмкцн цмумиляшмяляри Чебышев теореминин садя нятиъясидир: рийази эюзлямяси ЕХ олан Х тясадцфи кямиййяти Х ≥ 0 оларса, истянилян ε > 0 цчцн 

олар.