ЧЕБЫШЕВ ЧОХЩЯДЛИЛЯРИ – 1854 илдя П.Л. Чебышев тяряфиндян –1≤х≤1 парчасында тапылан ортогонал чохщядлиляр системи. Биринъи нюв Чебышев чох - щядлиляри ашаьыдакы дцстурла тяйин олунур:
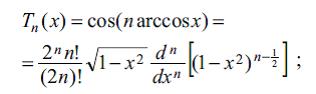
хцсуси щалда
![]()
олур.
Онлар –1≤х≤1 парчасында ![]() чякиси иля ортогоналдыр, йяни
чякиси иля ортогоналдыр, йяни
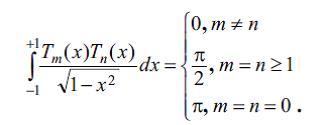
Биринъи нюв ![]() Ч.ч сыфырдан ян аз мейил едир. Бу о демякдир ки, ямсалы 1-дян бюйцк олан бцтцн н дяряъяли чохщядлиляр ичярисиндя мящз
Ч.ч сыфырдан ян аз мейил едир. Бу о демякдир ки, ямсалы 1-дян бюйцк олан бцтцн н дяряъяли чохщядлиляр ичярисиндя мящз ![]() максимум модулу –1≤ х≤1 парчасында ян кичик гиймятя маликдир, беля ки, бу максимум
максимум модулу –1≤ х≤1 парчасында ян кичик гиймятя маликдир, беля ки, бу максимум ![]() бярабярдир. й=Тн(х) Ч.ч. (1–х2)й″– хй′ +н2й=0 диференсиал тянлийини юдяйир вя онлар цчцн
бярабярдир. й=Тн(х) Ч.ч. (1–х2)й″– хй′ +н2й=0 диференсиал тянлийини юдяйир вя онлар цчцн ![]() рекуррент дцстуру доьрудур. Ун(х) икинъи нюв Чебышев чохщядлиляри –1≤х≤1 парчасында
рекуррент дцстуру доьрудур. Ун(х) икинъи нюв Чебышев чохщядлиляри –1≤х≤1 парчасында ![]() чякиси иля ортогоналдыр:
чякиси иля ортогоналдыр: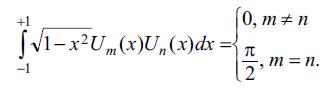
Онлар
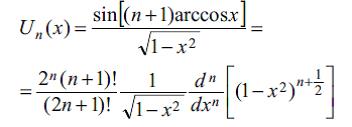
дцстуру иля тяйин олунур; хцсуси щалда У0(х)=1, У1(х)=2х, У2(х)=4х2–1, У3(х)=8х3–4х, У4(х)=16х4–12х2+1. Икинъи нюв Ч.ч. цчцн диференсиал тянлик вя
рекуррент дцстур ашаьыдакы шякилдя олар: (1–х2)й″–3хй′+н(н+2)й=0 Ун+1(х)=2хУн(х)– Ун–1(х). Биринъи вя икинъи нюв Ч.ч.
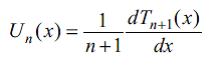
ифадяси иля ялагялидир.














