ЧЕВРЯ – бцтцн нюгтяляри верилмиш нюгтядян (Ч.-нин мяркязиндян) бярабяр мясафядя йерляшян гапалы мцстяви яйри; бу нюгтя яйри иля ейни мцстявидя йерляшир. Чеврянин мяркязини онун щяр щансы нюгтяси иля бирляшдирян парчайа Ч.-нин радиусу (Р) дейилир (шякил 1).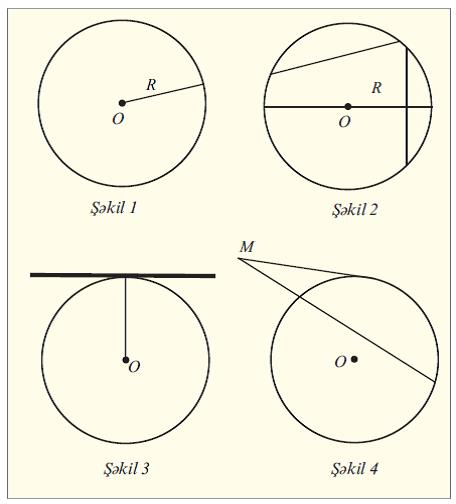
Чеврянин истянилян ики нюгтясини бирляшдирян парчайа вятяр дейилир (шякил 2). Мяркяздян кечян вятяр диаметр адланыр. Диаметр – ян узун вятярдир; вятярин ортасындан кечян диаметр она перпендикулйар олур. Ч. цзяриндя олан нюгтядян чевряйя йалныз бир тохунан чякмяк олар, бу тохунан щямин нюгтядян кечян радиуса перпендикулйардыр (шякил 3). Ч.-нин хариъиндя олан М нюгтясиндян чевряйя тохунан вя кясян чякилмишдирся, онда тохунанын квадраты кясянин юз хариъи щиссясиня щасилиня бярабярдир (шякил 4). Ч.-нин уз.-нун онун диаметриня нисбяти бцтцн чевряляр цчцн сабит кямиййятдир; бу нисбят транссендент ядяддир, йунан щярфи π (π=3,14159…) иля ишаря едилир (бах Пи). Чеврянин узунлуьу л=2πР дцстуру иля тяйин олунур. Мцстявинин Ч. иля ящатя олунан вя мяркязи Ч.-нин мяркязи иля цст-цстя дцшян щиссяси даиря адланыр. Аналитик щяндяся нюгтейи-нязяриндян Ч. дцзбуъаглы координат системиндя (х–а)2+(й–б)2 =Р2 шяклиндя тянликля тяйин олунан икинъи тяртиб мяркязи хятдир. Бурада а, б Ч.-нин мяркязинин координатларыдыр.

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, “Azərbaycan” xüsusi cildi (Azərbaycan dilində) |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2007 |
| ISBN: | 978-9952-441-01-7 |
| Səhifələrin sayı: | 881 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, I CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2009 |
| ISBN: | 978-9952-441-02-4 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, II CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2010 |
| ISBN: | 978-9952-441-05-5 |
| Səhifələrin sayı: | 604 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, III CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2011 |
| ISBN: | 978-9952-441-07-9 |
| Səhifələrin sayı: | 604 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, “Azərbaycan” xüsusi cildi (rus dilində) |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2012 |
| ISBN: | 978-9952-441-01-7 |
| Səhifələrin sayı: | 881 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, IV CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2013 |
| ISBN: | 978-9952-441-03-1 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, V CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2014 |
| ISBN: | 978-9952-441-10-9 |
| Səhifələrin sayı: | 592 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, VI CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2015 |
| ISBN: | 978-9952-441-11-6 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, IX CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2019 |
| ISBN: | 978-9952-441-17-8 |
| Səhifələrin sayı: | 600 |
ЧЕВРЯ – бцтцн нюгтяляри верилмиш нюгтядян (Ч.-нин мяркязиндян) бярабяр мясафядя йерляшян гапалы мцстяви яйри; бу нюгтя яйри иля ейни мцстявидя йерляшир. Чеврянин мяркязини онун щяр щансы нюгтяси иля бирляшдирян парчайа Ч.-нин радиусу (Р) дейилир (шякил 1).
Чеврянин истянилян ики нюгтясини бирляшдирян парчайа вятяр дейилир (шякил 2). Мяркяздян кечян вятяр диаметр адланыр. Диаметр – ян узун вятярдир; вятярин ортасындан кечян диаметр она перпендикулйар олур. Ч. цзяриндя олан нюгтядян чевряйя йалныз бир тохунан чякмяк олар, бу тохунан щямин нюгтядян кечян радиуса перпендикулйардыр (шякил 3). Ч.-нин хариъиндя олан М нюгтясиндян чевряйя тохунан вя кясян чякилмишдирся, онда тохунанын квадраты кясянин юз хариъи щиссясиня щасилиня бярабярдир (шякил 4). Ч.-нин уз.-нун онун диаметриня нисбяти бцтцн чевряляр цчцн сабит кямиййятдир; бу нисбят транссендент ядяддир, йунан щярфи π (π=3,14159…) иля ишаря едилир (бах Пи). Чеврянин узунлуьу л=2πР дцстуру иля тяйин олунур. Мцстявинин Ч. иля ящатя олунан вя мяркязи Ч.-нин мяркязи иля цст-цстя дцшян щиссяси даиря адланыр. Аналитик щяндяся нюгтейи-нязяриндян Ч. дцзбуъаглы координат системиндя (х–а)2+(й–б)2 =Р2 шяклиндя тянликля тяйин олунан икинъи тяртиб мяркязи хятдир. Бурада а, б Ч.-нин мяркязинин координатларыдыр.
ЧЕВРЯ – бцтцн нюгтяляри верилмиш нюгтядян (Ч.-нин мяркязиндян) бярабяр мясафядя йерляшян гапалы мцстяви яйри; бу нюгтя яйри иля ейни мцстявидя йерляшир. Чеврянин мяркязини онун щяр щансы нюгтяси иля бирляшдирян парчайа Ч.-нин радиусу (Р) дейилир (шякил 1).
Чеврянин истянилян ики нюгтясини бирляшдирян парчайа вятяр дейилир (шякил 2). Мяркяздян кечян вятяр диаметр адланыр. Диаметр – ян узун вятярдир; вятярин ортасындан кечян диаметр она перпендикулйар олур. Ч. цзяриндя олан нюгтядян чевряйя йалныз бир тохунан чякмяк олар, бу тохунан щямин нюгтядян кечян радиуса перпендикулйардыр (шякил 3). Ч.-нин хариъиндя олан М нюгтясиндян чевряйя тохунан вя кясян чякилмишдирся, онда тохунанын квадраты кясянин юз хариъи щиссясиня щасилиня бярабярдир (шякил 4). Ч.-нин уз.-нун онун диаметриня нисбяти бцтцн чевряляр цчцн сабит кямиййятдир; бу нисбят транссендент ядяддир, йунан щярфи π (π=3,14159…) иля ишаря едилир (бах Пи). Чеврянин узунлуьу л=2πР дцстуру иля тяйин олунур. Мцстявинин Ч. иля ящатя олунан вя мяркязи Ч.-нин мяркязи иля цст-цстя дцшян щиссяси даиря адланыр. Аналитик щяндяся нюгтейи-нязяриндян Ч. дцзбуъаглы координат системиндя (х–а)2+(й–б)2 =Р2 шяклиндя тянликля тяйин олунан икинъи тяртиб мяркязи хятдир. Бурада а, б Ч.-нин мяркязинин координатларыдыр.










