ДАЛЬАЛАР – фязада сонлу сцрятля йайылан вя маддя дашынмадан юзц иля енержи вя информасийа дашыйан щяйяъанланмалар. Мцхтялиф нюв дальа просесляри тябиятдя вя инсанын щяйатында сон дяряъя мцщцм рол ойнайыр. Мяс., Эцняшдян Йер сятщиня дахил олан енержи ясасян мцхтялиф диапазонлу електромагнит Д.-ы васитясиля ютцрцлцр. Ишыг шцаланмасына вя радиошцаланмайа эюря узаг космик обйектляр, о ъцмлядян “Каинатын кянарында” йерляшян обйектляр щаггында информасийа алырыг. Ъанлы орга- низмлярин синир телляри иля йайылан електрик импулслары дальа характери дашыйыр (бах Синир импулсу). Квант физикасында юйрянилян микрообйектляр йалныз зярряъик йох, щям дя дальа хассяляриня маликдир (бах Корпускулйар – дальа дуализми, де Бройл дальалары).

Гядим дюврлярдян бизя ян чох мялум олан дальалар – майе сятщиндяки дальалардыр; бцтювлцкдя майенин юзцнцн щярякятсиз гала билмясиня бахмайараг, онун сятщинин рягсляринин йердяйишмяси бу дальалар цчцн характерикдир. Майелярин вя газларын щяъминдя сыхылан вя сейрялян у з у н у н а еластики дальалар (акустик дальалар, о ъцмлядян сяс дальалары) йайыла биляр, бу заман мцщитин щиссяъикляринин йердяйишмяси Д.-ын йайылмасы истигамятиндя олур (шякил 1а). Бярк мцщитлярдя щямчинин ениня Д. да ола биляр, бу щалда йердяйишмя Д.-ын йайылма истигамятинин ениня олур (шякил 1б). Йерин бцтцн дяринлийиня нцфуз едян щяр ики нюв беля Д., зялзяля заманы баш верир. Симлярдяки вя миллярдяки Д. да ениня Д.-дыр. Д.-ын сонлу сцрятля йайылмасынын зярури шярти мцщитин инерсийасынын вя онун гоншу нюгтяляриндя параметрлярин дяйишмяляри арасында гайтарыъы гцввянин мейдана чыхмасына сябяб олан локал (йахынатясир) ялагянин олмасыдыр. Мяс., узунуна Д. щалында щяр щансы областда мцщитин сыхылмасы онда тязйигин йцксялмясиня вя щярякятин гоншу областа верилмясиня сябяб олур. Еластик Д. вя майе сятщиндяки Д. мцщитин щяйяъанланмасы иля (таразлыг щалынын позулмасы иля) йайылан Д.-дыр, лакин електрик вя магнит сащяляринин гаршылыглы ялагяли мякан-заман дяйишмялярини тясвир едян вя йайылма истигамятинин ениня олан електромагнит дальалары (ишыг, радиодальалар вя
б.) вакуумда да мювъуддур. Цмуми нисбилик нязяриййяси вакуумда гравитаси- йа дальаларынын да олмасыны мцмкцн сайыр.

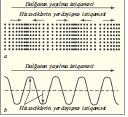 Шякил 1. Узунуна (а) вя ениня (б) дальалар.   

Фязанын бир нюгтясиндян диэяриня дальа щяйяъанланмаларынын дашындыьы бцтцн щалларда бу нюгтялярдяки сащяляр арасында сябяб-нятиъя ялагяляри баш верир, онларын йайылма сцряти ишыьын вакуумдакы ъ сцрятиндян бюйцк ола билмяз. Лакин хцсуси олараг мцяййян хятдя йерляшдирилмиш мянбялярин кюмяйи иля щямин хяттдя истянилян бюйцк сцрятля (о ъцмлядян ишыг сцрятиндян бюйцк) щярякят едян щяйяъанланмалар йаратмаг олар. Сырф кинематик мянада беля просесляри дя бязян Д. адландырырлар, лакин бу щалда енержи дашынмасы баш вермир вя динамик мянада щямин просес Д. дейил.

Гачан дальалар, фаза вя груп сцряти. Дальавари щярякятя ян садя вя типик мисал гачан дальалардыр; уйьун с динамик дяйишяни (мяс., сяс Д.-ында тязйиг) замандан (т) вя фяза координатларынын бириндян (х)

                                             с(х, т)=Ф(х – υт)

гануну иля асылыдыр, бурада Ф – ихтийари функсийадыр. х – υт=ъонст олдугда с кямиййяти сабит галыр вя Д.-ын бцтцн профили х бойунъа дяйишмяйян υ = Δx/Δt сцряти иля щярякят едир; бунлар стасионар Д. адланыр. υ-нин гиймяти конкрет дальа системиндян асылыдыр; мяс., кечириъи олмайан изотроп мцщитдя електромагнит дальалары цчцн υ=ъ/(εμ)1/2, бурада ε вя μ мцщитин диелектрик вя магнит нцфузлуьудур, майелярдя вя газларда сясин сцряти онларын адиабатик сыхылмасы иля тяйин едилир. с(х,т) ифадяси бирюлчцлц щал цчцн Даламбер тянлийи адланан

                                                                   д²с /дх² – υ^–2д²с/дт² = 0,
дальа тянлийинин щяллидир.

Реал дальа сащяляринин мякан-заман структуру айры-айры импулслар, дальа гошуму (тякрарланан щяйяъанланмаларын мящдуд сырасы) вя периодиклийя кифайят гядяр йахын олан мцхтялиф формаларда ола биляр. Синусоидала йахын (щармоник адланан) Д. хцсуси ящямиййятя маликдир вя эениш тятбиг едилир; бу щалда дальа сащясини характеризя едян динамик кямиййят 

                                       с(х,т)=А синφ(х,т),
                                       φ(х, т)=ωт–кх+φ₀

ифадяси иля тясвир олунур, бурада А – амплитуд (таразлыг вязиййятиндян олан ян бюйцк йердяйишмя), φ₀ – дальанын башланьыъ фазасы, ω = 2π/Т – рягслярин буъаг тезлийи, к=2π /λ – дальа ядяди, λ – дальа уз. (гоншу максимумлар вя минимумлар арасындакы мясафя), Т – периоддур (рягслярин там тсиклиня сярф олунан заман). Бу заман сабит φ(х,т)=ъонст фазалы нюгтяляр (дальа ъябщяси) υ_ф =ω/к=λ/Т фаза сцряти иля фязада йерлярини дяйишир. “Гачан” рягс структуруна охшарлыьыны нязярдя тутараг бязян дальалара рягслярин йайылмасы кими тяриф верирляр. Бир чох дальа системляриндя υ-нин гиймяти мцхтялиф тезликлярдя мцхтялифдир (дальаларын дисперсийасы баш верир), υ(ω) асылылыьы вя йа она еквивалент ω(к) мцнасибяти дисперсийа тянлийи адланыр.

Цмуми щалда мцстяви Д.-ын фазасыны бу шякилдя йазмаг олар: φ(р,т)=ωt–кр, бурада к – дальа вектору, р – фяза нюгтя- синин радиус-векторудур.

Практикада истифадя едилян Д. (сигнал лар) ъидди щармоник дейил: йа амплитуд, йа фаза, йа да тезлик Т вя λ мигйасында мцнтязям дяйишир (модулйасийа едир; бах Рягслярин вя дальаларын модулйасийасы), щям дя сигналын ютцрдцйц информасийа мящз модулйасийа гануну иля кодлашдырылыр. Дисперглянмиш (щяр щансы ъисмин ону ящатя едян мцщитдя назик-назик доьранмасы; дисперс системин алынмасы цсулларындан биридир) мцщитдя айры-айры спектрал гурумларын фаза сцрятляринин мцхтялифлийи она эятирир ки, сигналын гуршайаны цмуми щалда груп сцряти иля йайылыр вя фаза сцрятиндян фярглянир:

                                                                      υ_гр = дω /дк = υ–λдυ/дλ.

Мящз Д.-ын груп сцряти сигналын реал йайылма сцрятидир, о ъцмлядян енержинин дашынмасы, релйативист мящдудиййят мящз она аиддир (υгр<ъ); Д.-ын фаза сцряти ися принсипъя ишыьын сцрятиндян йцксяк ола биляр. Еля дальа системляри дя мцмкцндцр ки, фаза вя груп сцрятляри якс тяряфляря йюнялир, бунлар якс дальалар адланыр.

Дальаларын интерференсийасы. Истянилян тябиятли Д. интерференсийа етмяк габилиййятиня маликдир. Интерференсийа дедикдя, фязада бир-биринин цзяриня дцшян (топланан) ики вя йа даща чох Д.-ын гаршылыглы эцълянмяси вя йа зяифлямяси [фазаларын нисбятиндян (фяргиндян) асылы олараг] баша дцшцлцр. Ейни тезликли вя А₁ вя А₂ амплитудлу ики щармоник дальанын топланмасы областында онларын йекун интенсивлийи 

                                           A²=А²₁ +А²₂ +2А₁А₂ ъосΔφ

ифадясиня бярабярдир; Д.-ын там фазалар фярги (Δφ) фязанын мцхтялиф нюгтяляриндя мцхтялифдир. Δφ=0 (вя йа 2π ядядинин там мисилляри) олан нюгтялярдя йекун амплитуд амплитудларын ъяминя (А=А₁+А₂) бярабярдир, якс фазалы нюгтялярдя ися |А| =|А₂ – А₁|, (А₁=А₂ олдугда) бу нюгтялярдя бир дальа о бири дальаны тамамиля “сюндцрцр”. Нятиъядя фязада рягс интенсивликляринин, структуру, интерференсийа едян дальаларын фаза ъябщяляринин формасындан асылы олан минимум вя макс.-лары йараныр (шякил 2). Фактики олараг бу, дальа сащясинин енержисинин фязада йенидян пайланмасыны эюстярир.

 Шякил 2. Ики нюгтяви мянбядян чыхан дальаларын интерференсийасы.

Интерференсийа мянзяряляринин мцшащидяси цчцн дальаларын кощерентлийи мцщцм ящямиййят дашыйыр.

Гейри-биръинс мцщитляр, дальаларын сынмасы вя якс олунмасы. Мцстяви гачан дальалар, ъидди йанашылдыгда, йалныз биръинс фязада мювъуд ола билир. Ики мцщити айыран кяскин сярщяд олдугда (λ дальа уз. мигйасында) дальаларын якс олунмасы (гайытмасы) вя дальаларын сынмасы (икинъи мцщитя кечмяси) баш верир (шякил 3). Яэяр дцшян Д. вя сярщядин юзц мцстявидирся, онда кечян вя якс олунан Д. да мцстяви олаъаг. Бу Д.-ын параметрляри арасындакы ялагя мцвафиг дальа сащясинин динамик тянликляриндян чыхан сярщяд шяртляри иля тяйин едилир. Изотроп мцщитлярдя α_я яксолунма буъаьы α₀ дцшмя буъаьына бярабярдир, α_с сынма буъаьы ися Снелл ганунуну юдяйир: υ₂синα₀ =υ₁синα_с. Кечириъи олмайан вя магнитсиз мцщитдя електромагнит Д. цчцн яксолунма вя сындырма ямсаллары Френел дцстурлары иля тяйин олунур. Бу ямсаллар дцшян Д.-ын мцхтялиф полйаризасийалары цчцн мцхтялифдир.

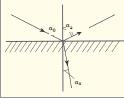 Шякил 3. Ики мцщити айыран мцстяви сярщяддя якс олунан вя сынан дальалар.

Мцщит мцнтязям гейри-биръинс оларса, дальа сащясини “квазимцстяви” щесаб етмяк олар, йяни бу щалда λ тяртибли мясафялярдя А амплитудунун вя к дальа векторунун дяйишмяляри кифайят гядяр кичик олаъаг. Беля щалларда щяндяси оптикадан эениш истифадя едилир ки, бунун да ясасында сярбяст шцалар дясти шяклиндя олан дальа сащясинин тясвири дурур. Изотроп мцщитдя шцанын истигамяти к дальа вектору иля цст-цстя дцшцр, гейри-биръинс мцщитдя шцанын мцнтязям сынмасы рефраксийа адланыр. “Щяндяси оптика” термини адятян йалныз ишыг Д.-ы цчцн йох, щям дя истянилян тябиятли Д. цчцн дя ишлядилир (акустикада аноложи йахынлашма щяндяси акустика адланыр).

Дальа дястяляри. Дальаларын дифраксийасы. Щяндяси оптиканын ганунларына эюря архасында йарыьы олан гейри-шяффаф екрана мцстяви Д.-ын дцшмяси заманы ишыьы вя кюлэяси кяскин сярщядя малик д ениндя паралел дястяляр йайылмалыдыр. Лакин беля нятиъя Д.-ын физики тябиятиндян асылы олмайараг екрана гядяр олан мясафя йалныз р < д²/λ тяртибиндя оланда доьрудур (бу област йахын зона адланыр). Бюйцк мясафялярдя дястянин вязиййяти дяйишмяйя башлайыр – дальа сащяси щяндяси кюлэя зонасына “эирир”, “ишыглы” областда ися интенсивлийин максимумлары вя минимумлары мейдана эялир. Щяндяси оптиканын ганунларындан кянара чыхан бу щадисяляр дальаларын дифраксийасы адланыр. р >>д²/λ олдугда (Фраунщофер дифраксийасы) дальа ъябщяси, дястянин буъаг енлийи α=λ/д олан локал сферик олур. Дифраксийа щадисясинин сябяби ондан ибарятдир ки, идеал мцстяви Д.-дан фяргли олараг ениня мящдуд дястя юз фяза спектриндя λ / 4 тяр- тибли буъаг сяпилмясиня малик дальа векторлары пакети сахлайыр. Дифраксийа мясяляляринин тяхмини щялли цчцн Щцйэенс-Френел принсипи ялверишлидир вя эениш тятбиг олунур. Бу принсипя эюря мянбядян кянарда олан ихтийари нюгтядяки дальа сащяси биринъи (ясас) мянбяни ящатя едян гапалы сятщдя йерляшян икинъи мянбялярин Д.-ынын суперпозисийасы шяклиндя тапыла биляр (онларын интерференсийасыны нязяря алмагла); илкин (ишыгландыран) дальа иля мцшащидя нюгтяси арасындакы йолда гейри-шяффаф екран олар- са, икинъи мянбялярин амплитуду мцвафиг нюгтялярдя сыфра бярабяр гябул едилир. Шякил 4-дя гейри-шяффаф екранын кянарындан мцшащидя олунан ишыьын дифраксийасынын мянзяряси эюстярилмишдир. Фраунщофер дифраксийасы заманы йаранан кяскин максимумлары дифраксийа гяфясляриндян истифадя етмякля мцяййян бир формайа салмаг олар. Беля гяфясляр спектрал ъищазлар кими истифадя едилир. Даща эениш мянада истянилян гейри-биръинсликляри (о ъцмлядян λ-дан кичик) сахлайан мцщитлярдя Д.-ын йайылмасы заманы ямяля эялян бцтцн еффектляр дифраксийайа аиддир.

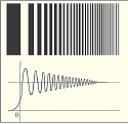 Шякил 4. Йухарыда – екранын кянарындан ишыьын дифраксийасы (ишыгдан кюлэяйя доьру мцряккяб кечид эюрцнцр); ашаьыда – ишыг вя кюлэя арасындакы фязанын ишыгланма дяряъясини характеризя едян яйри (екранын кянары координат башланьыъына уйьундур).

Дальаларын шцаланмасы. Доплер еффекти. Дальа системини (мцщити, сащяни) таразлыг щалындан чыхаран истянилян хариъи тясир дальа мянбяйи ола биляр; бу заман щяйяъанланан Д. мянбянин сярф етдийи енержини дашыйыр. Еластики мцщитдя рягс едян ъисим акустик Д. шцаландырыр, дяйишян ъяряйанлар, йяни тяъилля щярякят едян йцкляр, мяс., дипол моменти замандан асылы олараг периодик дяйишян електрик диполу електромагнит Д.-ынын мянбяйидир. Цмцми щалда шцаланма енержиси мцхтялиф истигамятляр цзря гейри-бярабяр пайланыр.

Д.-ын шцаланмасы ъисмин щяр щансы мцщитдя, Д.-ын бу мцщитдяки йайылма сцрятиндян бюйцк бярабярсцрятли щярякяти заманы да мцмкцндцр.

Д. мянбяйи вя онларын гябуледиъиси (мцшащидячи) щярякятсиз оларса, хятти мцщитдя гябул едилян Д.-ын тезлийи мянбянин тезлийи иля цст-цстя дцшцр. Мянбя щярякят етдикдя щярякятсиз мцшащидячинин гябул етдийи Д.-ын тезлийи мянбянин щярякят истигамятиндян асылы олур. Мянбянин щярякятсиз мцшащидячийя доьру щярякяти заманы (вя йа мцшащидячинин тярпянмяз мянбяйя доьру) гябуледилян ω тезлийи тярпянмяз мянбя заманындакы ω₀ тезлийиндян бюйцк олаъаг; мянбянин мцшащидячидян узаглашдырмасы заманы онун гябул етдийи шцаланманын тезлийи аз олаъаг. Д. мянбяйинин вя мцшащидячинин гаршылыглы щярякяти заманы тезлийин беля дяйишмяси Доплер еффекти адланыр. Бу кинематик еффектдир вя истянилян физики тябиятли Д. цчцн баш верир.

Д.-ын тезлийинин дяйишмяси онларын, параметрляри замана эюря дяйишян гейри-стасионар мцщитдя йайылмасы заманы да мцмкцндцр. Мяс., гаршысына эялян сярщяддян якс олунан Д.-ын тезлийи йцксялир. Гейри-хятти дальалар. Д.-ын кифайят гядяр бюйцк амплитудларында мцхтялиф гейри-хятти еффектляр ямяля эялмяйя башлайыр (бах Гейри-хятти оптика, Гейри-хятти акустика). Мяс., дайаз судакы сятщ Д.-ынын габарыглыгларынын (ляпяляринин) сцряти чюкцклцкляринин (батыгларынын) сцрятиндян бюйцк олур, она эюря дя онларын йайылмасы заманы юн ъябщянин бурулмасы баш верир ки, бу да сон нятиъядя онларын даьылмасына эятирир. Акустик Д.-ын охшар гейри-хятти трансформасийасы зярбя Д.-ынын йаранмасына эятирир, лакин яввялъя синусоидал профил мцяййян мясафядя мишар формасыны алыр (шякил 5). Дисперсийасыз башга системлярдя дя мцмкцн олан Д. профилинин охшар трансформасийасы онун спектриндя чохлу сайда йцксяк щармонийаларын мейдана эялмясини эюстярир. Нязярячарпан дисперсийанын мювъудлуьу шяраитиндя сычрайыш формалы ъябщялярин йаранмасы артыг мцмкцн олмур вя гейри-хяттилик вя дисперсийанын параметрляринин нисбятиндян асылы олан Д.-ын гейри-хятти инкишафы даща мцряккяб характер дашыйыр. Мцяййян шяраитлярдя, профили кичик амплитудларда синусоидя, бюйцк амплитудларда ися гыса импулслар ардыъыллыьына йахын олан стасионар гачан Д. мювъуд ола биляр. Сонсуз период щяддиндя тяклянмиш Д.–солитонлар алыныр, онларын амплитудлары йцксяк олдугъа, гысамцддятли вя бюйцк йайылма сцрятиня малик олур.

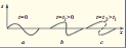 Шякил 5. Садя дальанын инкишафы (а), “шишмянин”ямяля эялмяси (б) вя зярбя дальасынын партламасы (парчаланмасы) (ъ).

Гейри-хяттилик дальа дястяляринин йайылмасына ящямиййятли дяряъядя тясир едя билир.

Фязада ики интенсив дальа (о ъцмлядян мцхтялиф тябиятли) бир-бирини юртярся, онларын гейри-хятти гаршылыглы тясири баш верир. Гейри-хятти просесляр актив мцщитлярдя, йяни баш верян дальа щяйяъанланмаларынын удулмадыьы, яксиня эцъляндийи мцщитлярдя (хцсуси щалда лазерлярдя) мцщцм ящямиййятя маликдир. Мящз гейри-хятти факторлар, дисперсийа иля йанашы, беля системлярля щяйяъанландырылан рягслярин амплитудуну, формасыны вя спектрини тяйин едир. Мцяййян шяраитлярдя бу рягсляр гейри-мцнтязям (хаотик) ола биляр (бах Динамик хаос ).

Яд.: Г о р е л и к  Г.С. Колебания и волны. 2­е изд. М.,1959; В и н о  г р а д о в а  М.Б., Р у д е н к о О.В., С у х о р у к о в А.П. Теория волн. 2­е изд. М., 1990; Р ы с к и н Н.М., Т р у б е ц к о в Д.И. Нелинейные волны. М., 2000; Т р у б е   ц   к   о  в Д.И., Р  о  ж н е в  А.Г. Линейные колебания и волны. М.,2001.