ДАЛЬАЛАРЫН ДИФРАКСИЙАСЫ – дальаларын йайылмасы заманы щяндяси оптика ганунларындан истянилян кянарачыхмалар. Беля цмуми анламда Д.д.-ны дальаларын гейри-биръинс мцщитдя йайылмасы вя сяпилмяси щадисяляриндян фяргляндирмяк олмур. Дифраксийа заманы дальалар щяндяси кюлэя областына дцшя билир: манеяни гуршамаг, сятщ бойунъа узаныб эетмяк, кичик йарыглардан кечяряк екранлара йайылмаг вя с. Мяс., радиодальа щятта ионосфердян якс олунмадан беля, цфцг архасына кечя, сяс ися евин арха кцнъцндян ешидиля биляр.
Ишыг цчцн Д.д.-нын илк дальа трактовкасыны биринъи олараг Т.Йунг (1800), икинъи ися О. Френел (1815–18) вермишдир. Йунг щесаб едирди ки, манеяйя эюря йаранан дальа сащясинин мянзяряси мящз дальаларын дифраксийасы вя интерференсийасынын бирляшмясидир. О, Д.д.-ны изащ етмяк цчцндальаларын, шцаларын истигамятиндяки ади йайылма ганунларындан башга, рягслярин амплитудунун дальа ъябщяляри бойунъа ениня верилмяси (ениня диффузийа) принсипини дахил етмиш вя эюстярмишдир ки, бу верилмянин сцряти дальа уз. вя ъябщядя амплитудларын дцшэцсц иля мцтянасибдир. Йунга эюря, дифраксийайа уьрамыш дальа манеянин кянары архасындакы кюлэянин сярщядинин мцяййян ятрафында локал баш верир. Аналожи дифраксийайа уьрамыш дальа, ишыглы областда да йараныр, беля ки, бцтювлцкдя санки С манеясинин сятщинин кянарындан бурахылан силиндрик дальа сащяси формалашыр (шякил 1). Дифраксийайа уьрамыш дальаларын дцшян дальанын манея иля юртцлмяйян габаг щиссяси иля интерференсийасы Б′ екранында ББ′ кюлэясинин сярщядиндян йухарыда йерляшян интерференсийа золагларынын ямяля эялмясини, ашаьы щиссядя ися онларын олмадыьыны эюстярир.
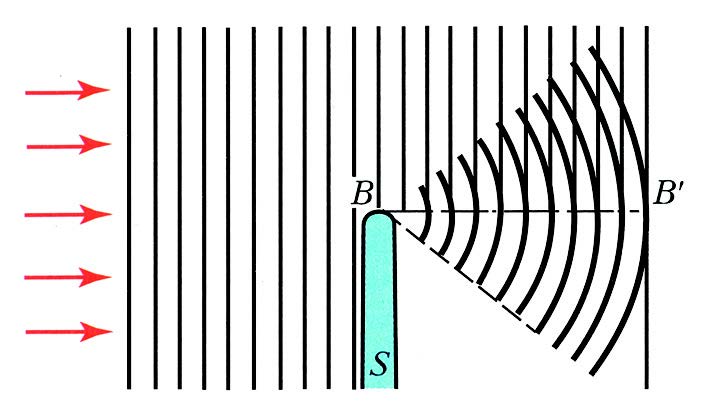Шякил 1. Йунга эюря дальаларын екран кянарындан дифраксийасы схеми.
О. Френел Йунгун локал йанашмасындан имтина етди вя Щцйэенс принсипиня (1690) ясасланараг юзцнцн интеграл методуну тяклиф етди (бах Щцйэенс–Френел принсипи). Френеля эюря, дифраксийа сащяси, манея иля юртцлмяйян дцшян дальа ъябщяси щиссяси бойунъа пайланмыш гондарма икинъи мянбялярин сащяляринин интерференсийасынын нятиъяси кими тясвир олуна биляр (шякил 2). Френел икинъи мянбялярин олдуьу сятщи Френел зоналары дейилян йарымдальа зоналарына айырды (шякил 3). Д.д.-нын характери йарыгда нечя зонанын йерляшмясин- дян вя йа биринъи Френел зонасынын юлчцсцнцн йарыьын а радиусуна нисбятиня бярабяр п Френел (дальа) параметриндян асылыдыр: п=√λz /а (з – мцшащидя нюгтясинин коор- динаты, λ – дальа узунлуьу). п кямиййятиндян асылы олараг Д.д.-нын ашаьыдакы областларыны фяргляндирирляр: щяндяси оптика вя йа прожектор областы, п ≪1; Френел дифраксийасы областы, п 1 тяртибиндядир; Фраунщофер дифраксийасы областы, п≫1. а вя λ-нын гейд едилмиш гиймятляриндя бу областлар мцшащидя нюгтясинин йарыгдан узаглашмасы сырасында (йяни з-ин артмасы иля) ардыъыл йерляшмишдир. Йарыьа йапышан биринъи областда (з≪а2λ) амплитудун ениня пайланмасы амплитудун йарыьын юзцндя пайланмасыны тякрар едир вя щяндяси оптика йахынлашмасына уйьун олур. Икинъи зонада (з, а2/λ тяртибиндядир) амплитудун ениня пайланмасы хейли дяряъядя позулур. Бу мясафялярдян башлайараг дальа дястяси нисбятян тез эенишлянир (дифраксийа сябябиндян). Цчцнъц, узаг областда (з≫а2λ) дифраксийа сащяси мцяййян истигамятя малик локал мцстяви структурлу даьылан сферик дальаны тясвир едир.
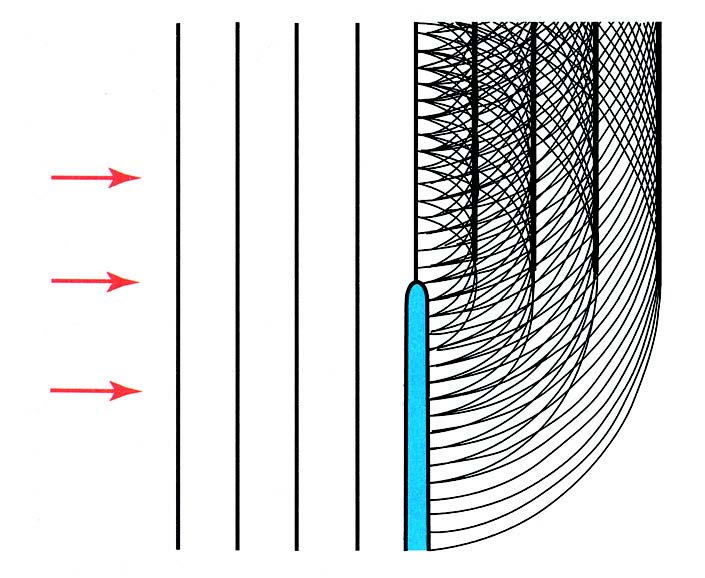Шякил 2. Френеля эюря дальаларын екран кянарындан дифраксийасы схеми.
Сонралар эюстярилмишдир ки, бярабяр шяртлярдя щяр ики йанашма ейни нятиъяляря эятирир, лакин конкрет бахылмалар заманы онлардан бириня методики цстцнлцк вериля биляр. Гейд етмяк лазымдыр ки, Йунгун эениш шякилдя инкишаф етдирдийи ениня диффузийа методу, ясасян гыса електромагнит дальалары диапазонларынын истифадяси (мазерлярин, лазерлярин вя с. мейдана чыхмасы) вя мцвафиг “електродинамик тяминатын” зярурилийи иля баьлыдыр (бах Квазиоптика). Бундан башга, бу методун юз-юзцня фокусланма типли бязи гейри-хятти дифраксийа вя електромагнит дальаларынын юз-юзцня каналлашма мясяляляриня адекват олмасы мялум олду.
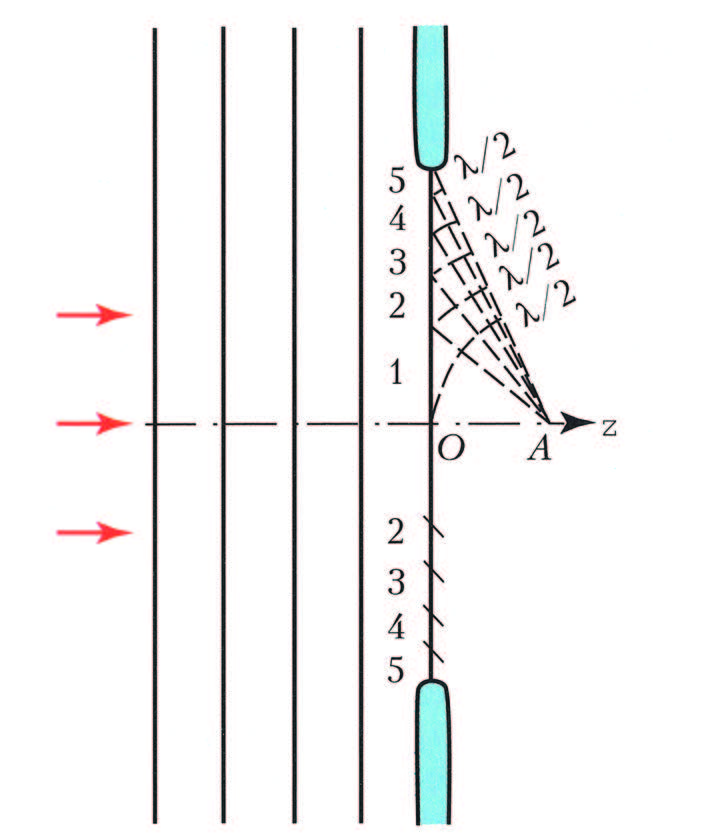Шякил 3. Френеля эюря йарыьын архасында дифраксийа мянзярясинин гурулушу (Френел зоналарына бюлцнмя).
Квант механикасы обйектляри дальа тябиятиня хас олдуьуна эюря дифраксийа щадисяси микроалямдя дя баш верир (бах Зярряъиклярин дифраксийасы).
Яд.: Ф о к В.А. Проблемы дифракции и распространения электромагнитных волн. М., 1970; Боровик ов В. А., Кинбер Б.Е. Геометри ческая теория дифракции. М., 1978; Ваганов Р.Б., К аценеленбаум Б.З. Основы теории дифракции. М.,1982.
