ДЕКАРТ КООРДИНАТ СИСТЕМИ –мцстявидя вя йа фязада дцзхятли координат системи; нюгтянин вязиййяти бир нюгтядя кясишян гейд едилмиш дцз хятляр цзяриндяки пройексийасы иля тяйин едилир. Дцз хятлярин кясишдийи нюгтя координат башланьыъы, бу пройексийалар нюгтянин координатлары, дцз хятляр ися координат охлары адланыр.
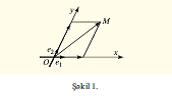
Цмуми щалда мцстяви цзяриндя Д.к.с. О нюгтяси (координат башланьыъы) вя она тятбиг едилян бир дцз хятт цзяриндя йерляш- мяйян низамланмыш е1 вя е2 векторлары (базис векторлар) иля верилир. Координат башланьыъындан базис векторлар истигамятиндя кечян дцз хятляря верилмиш Д.к.с.-нин координат охлары дейилир. е1 вектору иля тяйин олунан биринъи дцз хяття абсис оху (вя йа Ох оху), икинъийя ися ординат оху (вя йа Ой оху) дейилир. Д.к.с. юзц Ое1е2 вя йа Охй иля ишаря олунур. Ое1е2 Д.к.с.-ндя (шякил 1) М нюгтясинин координатлары OM¯векторунун {е1,е2} базиси цзря айрылышын- дакы ямсаллар, йяни низамланмыш (х,й) ядядляр ъцтцдцр, х вя й елядир ки, OM¯ =хе1+йе2. х ядяди (–∞<х<∞) М нюгтясинин абсиси, й ядяди (–∞<й<∞) ися М нюгтясинин ординаты адланыр. Яэяр (х,й)
М нюгтясинин координатларыдырса, онда М(х,й) йазылыр.
Тутаг ки, мцстяви цзяриндя ики Ое1е2 вя О′e′1 e′2 Д.к.с.-ляри верилмишдир, {e′1 ,e′2 } базис векторлары e′1 = a11e1 + a12e2 , e′2 = a21e1 + a22e2 дцстурлары васитясиля {е1,е2} базис векторлары иля ифадя олунур вя Ое1е2 Д.к.с.-ндяки О′ нюгтясинин координатлары (х0,й0)-дыр, онда Ое1е2 Д.к.с.-ндяки М нюгтясинин (х,й) координатлары вя щямин нюгтянин О′e′1 e′2 Д.к.с.-ндяки координатлары ашаьыдакы мцнасибятлярля ялагялидир:
x = a11x′ +a21y′+x0 ,
y = a12x′ +a22y′+y0 .
Яэяр {е1,е2} базиси ортонормаллашдырылмышдырса, йяни е1 вя е2 векторлары бир-бириня перпендикулйардырса вя узунлугларыващидя бярабярдирся (бу щалда е1 вя е2 орт векторлардыр) онда бу, дцзбуъаглы Д.к.с. адланыр. Дцзбуъаглы Д.к.с.-ндя М нюгтясинин х вя й координатлары М нюгтясинин уйьун олараг Ох вя Ой охлары цзяриндяки ортогонал пройексийаларыдыр. Охй дцзбуъаглы Д.к.с.-ндя М1(х1,й1) вя М2(х2,й2) нюгтяляри арасындакы мясафя ![]() ифадясиня бяраbərdir.
ифадясиня бяраbərdir.

Бир Охй дцзбуъаглы Д.к.с.-ндян диэяр О′х′й′ дцзбуъаглы Д.к.с.-ня кечид дцстуру ашаьыдакы кимидир:
x = x′cosα – y′sinα +x0 , y = x′ sinα+ y′cosα+y0
вя йа
x = x′cosα + y′sinα +x0 , y = x′ sinα – y′cosα+y0 .
Биринъи щалда О′х′й′ системи е1 вя е2 векторларынын α буъаьы гядяр дюнмяси вя О координат башланьыъынын О′ нюгтясиня кючцрцлмяси васитясиля (шякил 2), икинъи щалда ися е1 вя е2 векторларынын α буъаьы гядяр дюнмяси, е2 векторуну сахлайан дцз хяттин е1 векторуну сахлайан дцз хяття нязярян пройексийасы вя О координат башланьыъынын О′ нюгтясиня кючцрцлмяси васитясиля йараныр (шякил 3).

Бязян базис векторлар арасындакы буъаг дцз буъаг олмайан корбуъаглы Д.к.с.-ндян дя истифадя олунур.
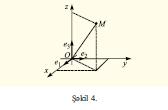
Аналожи олараг фязада цмуми Д.к.с. тяйин едилир: координат башланьыъы олан О нюгтяси, бу нюгтядян чыхан вя бир мцстяви цзяриндя йерляшмяйян е1,е2,е3 векторлар цчлцйц (базис векторлар) верилир. Мцстяви щалында олдуьу кими координат охлары – абсис оху (Ох оху), ординат оху (Ой оху) вя аппликат оху (Оз оху) тяйин олунур (шякил 4). Фязада Д.к.с. Ое1е2е3 (вя йа Охйз) иля ишаря олунур. Координат охлары ъцтцндян кечян мцстявиляр координат мцстявиляри адланыр. Яэяр Оз-ин мцсбят йарымохунун щяр щансы нюгтясиндян Охй мцстявисиня бахдыгда, Ох охундан Ой охуна фырланма саат ягрябинин яксиня оларса, онда Д.к.с. фязада саь Д.к.с., якс щалда, сол Д.к.с. адланыр. Яэяр е1,е2,е3 базис векторларынын узунлуьу ващидя бярабярдирся вя онлар ъцт-ъцт перпендикулйардырса, онда Д.к.с.-ня дцзбуъаглы Д.к.с. дейилир. Фязада ейни орийентасийалы бир Д.к.с.-нин диэяр Д.к.с.-ня нязярян вязиййяти цч Ейлер буъаьы васитясиля тяйин едилир.
Р.Декартын “Щяндяся” ясяриндя (1637), нюгтяляринин координатлары йалныз мцсбят олан корбуъаглы координат системиндян данышылмасына бахмайараг, Д.к.с. онун ады иля адландырылмышдыр. “Щяндяся”нин 1659–61 иллярдяки няшриня щолланд рийазиййатчысы И.Гудденин илк дяфя олараг координатларын щям мцсбят, щям дя мянфи ядядляр олмасыны мцмкцн щесаб едян иши дахил едилмишдир. Фяза Д.к.с.-ни франсыз рийазиййатчысы Ф.Лаир (1679) елмя дахил етмишдир. 18 ясрин яввялляриндя Декарт координатлары цчцн х, й, з ишаряляри мцяййян едилмишдир.














