ENTROPİYA (yun. έnτροπία – çevrilmә) – termodinamik sistemin hal funksiyası; enerjinin sәpilmәsinin dönmәzlik hәddini tәyin etmәk üçün ilk dәfә termodinamikaya daxil edilmiş anlayışdır. “E.” anlayışını termodinamikaya alman alimi R. Klauzius (1865) daxil etmişdir. O göstәrmişdir ki, istiliyin işә çevrilmәsi prosesi E.-nı daxil etmәklә dәqiq riyazi şәkildә ifadә edilә bilәn ümumi fiziki qanunauyğunluğa – termodinamikanın ikinci qanununa tabe olur. Mәs., tsiklik prosesi kvazi statik (sonsuz yavaş) yerinә yetirәn termodinamik sistem üçün (mütlәq temp-run (T) uyğun qiymәtlәrindә sistem ardıcıl olaraq δQ istilik miqdarı alır) “gәtirilmiş” istilik miqdarının δQ/T bütün tsikl üzrә inteqralı sıfıra bәrabәrdir
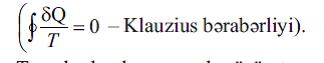
Tarazlıqda olan proseslәr üçün termodinamikanın ikinci qanununa ekvivalent olan bu bәrabәrliyi Klauzius ixtiyari tsiklik prosesә sonsuz böyük sayda elementar Karno tsikllәrinin cәmi kimi baxmaqla almışdır. Klauziusun riyazi bәrabәrliyi
![]()
ifadәsinin “E.” adlanan S hal funksiyasının tam diferensialını tәsvir etmәsi üçün zәruri vә kafidir (E.-nın diferensial tәyini). İxtiyari iki A vә B hallarında (mәs., temp-r vә hәcmin verilәn qiymәtlәrindә) sistemin E.-ları fәrqi
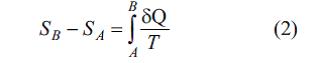
(E.-nın inteqral tәyini). Burada inteqrallama A vә B hallarını әlaqәlәndirәn istәnilәn kvazistatik prosesin yolu boyunca aparılır vә Klauzius bәrabәrliyinә görә ΔS = SB – SA E. artımı inteqrallama yolundan asılı deyil. Belәliklә, termodinamikanın ikinci qanunundan belә nәticә çıxır ki, kvazistatik adiabatik proseslәrdә (δQ = 0) sabit qalan birqiymәtli S hal funksiyası mövcuddur. E.-nın sabit qaldığı proseslәr izoentropik proseslәr adlanır. Termodinamikanın birinci qanununa görә δQ = dU + pdV, yәni sistemә verilәn istilik miqdarı daxili enerji artımına (dU ) vә sistemin gördüyü elementar pdV işinә bәrabәrdir, burada p – tәzyiq, V – sistemin hәcmidir. Termodinamikanın birinci qanunu nәzәrә alındıqda E.-nın diferensial tәnliyi
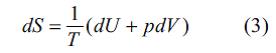
şәklini alır. Buradan belә nәticә çıxır ki, daxili enerji (U) vә hәcm (V ) sәrbәst dәyişәnlәr kimi seçildikdә E. termodinamik potensialı ifadә edir. E.-nın xüsusi törәmәlәri T vә p ilә aşağıdakı ifadәlәrlә әlaqәlidir:
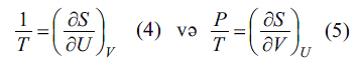
(4) vә (5) ifadәlәri sistemin hal tәnliyini (birinci – kalorik, ikinci – termik) tәyin edir. (4) tәnliyi mütlәq temperaturun tәyininin әsasını tәşkil edir (bax hәmçinin Temperatur, Temperatur şkalası). (2) düsturu E.-nı yalnız additiv sabit dәqiqliyinә qәdәr tәyin edir (yәni E.-nın hesablanma başlanğıcını ixtiyari saxlayır). E.-nın mütlәq qiymәtini termodinamikanın üçüncü qanununun kömәyi ilә müәyyәn etmәk olar (bu qanunda E.-nın hesablan masının başlanğıc nöqtәsini T = 0-da S0 = 0 qәbul edirlәr). E. anlayışının dönmәyәn (tarazlıqda olmayan) proseslәrin analizi üçün mühümlüyü dә ilk dәfә Klauzius tәrәfindәn göstәrilmişdir. Dönmәyәn proseslәr üçün gәtirilmiş istilikdәn (δQ ⁄ T ) qapalı yol üzrә inteqral hәmişә mәnfidir:
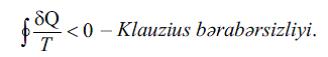
Bu bәrabәrsizlik Karno teoreminin nәticәsidir: qismәn vә ya tam dönmәyәn tsiklik prosesin f.i.ә. dönәn tsiklik prosesin f.i.ә.-ndan hәmişә kiçikdir. Klauzius bәrabәrsizliyindәn çıxır ki,
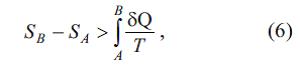
ona görә dә adiabatik izolәedilmiş sistemin E.-sı dönmәyәn proseslәrdә yalnız arta bilәr. Belәliklә, E. adiabatik şәraitlәrdә proseslәrin xarakterini müәyyәn edir: yalnız elә proseslәr mümkündür ki, E. ya dәyişmәz qalır (dönәn proseslәr), ya da artır (dönmәyәn proseslәr). Bu zaman prosesdә iştirak edәn cisimlәrdәn hәr birinin E.-sının artması vacib deyil, prosesin dәyişiklik әmәlә gәtirdiyi cisimlәrin E.-sının ümumi cәmi artır. Adiabatik sistemin termodinamik tarazlığına E.-nın maksimum halı uyğun gәlir. E. bir deyil, bir neçә maks.-a malik ola bilәr, bu zaman sistem bir neçә tarazlıq halında olur. E.-nın daha böyük maks.-una uyğun gәlәn tarazlıq mütlәq dayanıqlı (stabil) tarazlıq adlanır. Adiabatik sistemin E.-sının tarazlıq halındakı maksimumluq
şәrtindәn mühüm nәticә çıxır: sistemin bütün hissәlәrinin temp-ru tarazlıq halında eynidir. Əgәr termodinamik qeyri-tarazlıq halı termodinamik tarazlıq halından az fәrqlәnәrsә, E. anlayışını bu hala da tәtbiq etmәk olar vә kiçik, lakin hәlә ki, makroskopik olan hәcmlәrdә lokal termodinamik tarazlıq haqqında tәsәvvürü daxil etmәk olar. Tarazlıqda olmayan sistemin bütövlükdә E.-sı onun lokal tarazlıqda yerlәşәn hissәlәrinin E.-ları cәminә bәrabәrdir.
Tarazlıqda olmayan proseslәrin termodinamikası vahid hәcmdә vә vahid zamanda termodinamik tarazlıqdan kәnara çıxması sәbәbindәn yaranan E.-nın artması prosesini daha dәqiq öyrәnmәyә vә E.-nın miqdarını hesablamağa imkan verir. Statistik fizika E.-nı sistemin verilәn makroskopik halının hәyata keçirilmәsi ehtimalı ilә әlaqәlәndirir. E. verilәn tarazlıq halının statistik çәkisinin (Ω) loqarifmi ilә tәyin edilir:
![]()
burada Ω(ε, N) – N zәrrәciklәrdәn ibarәt sistemin ε enerjisinin qiymәtlәri yaxınlığında Δε enerjisinin dar intervalındakı kvantmexaniki sәviyyәlәrin sayıdır.
E.-nın sistemin halının ehtimalı ilә әlaqәsi ilk dәfә 1872 ildә Avstriya fiziki L.Boltsman tәrәfindәn müәyyәn edilmişdir: sistemin E.-sının artması onun ehti -
malının az olan haldan çox olan hala keç mәsi ilә şәrtlәnir. Termodinamikadan fәrqli olaraq statistik fizika proseslәrin xüsusi sinfini – fluktuasiyaları öyrәnir. Bu halda sistem ehtimalı daha çox olan haldan ehtimalı daha az olan hala keçir vә onun E.-sı azalır. Fluktua siyanın mövcudluğu göstәrir ki, böyük zaman fasilәsindә E.-nın artması qanunu yalnız orta hesabla yerinә yetirilir. Tarazlıqda olmayan sistem tarazlığa gәlincә arasıkәsilmәdәn E.-sı az olan haldan E.-sı çox olan hala keçir vә nәhayәt, tarazlıqda әn böyük qiymәt alır. Qapalı sistem müәyyәn anda qeyri-tarazlıq halındadırsa, ondan sonrakı anlar üçün әn ehtimallı hala sistemin E.-sının monoton artması uyğun gәlir. Kainatı vahid bir qapalı sistem qәbul edib, termodinamikanın ikinci qanununu tәtbiq etsәk, tәcrübә ilә nәzәriyyә arasında kәskin ziddiyyәt aşkara çıxar. Nәzәriyyәyә görә, vahid qapalı sistem kimi fәrz olunmuş Kainat gec-tez istilik ta razlığına gәlmәlidir. Buna Kainatın “istilik ölümü” deyilir. Gündәlik astro nomik mü şahidәlәr isә bunu tәsdiq etmir. Bu ziddiyyәt Kainatın vahid bir qapalı sistem kimi qәbul edilmәsi nәticәsindә alınır. Ümumi nisbilik nәzәriyyәsinә görә, Kainat zaman vә koordinata görә dәyişәn qravitasiya sahәsindә olduğundan heç vaxt vahid bir sistem kimi qapalı hesab edilә bilmәz. E. anlayışı elmin digәr sahәlәrindә dә (biologiyada, informasiya nәzәriyyә sindә, hesablama texnikasında vә s.) var.














