ДИФЕРЕНСИАЛ ЩЕСАБЫ – рийази анализин тюрямя, диференсиал вя онларын функсийаларын тядгигиня тятбигини юйрянян бюлмяси.

Д.щ. щягиги ядяд, функсийа, лимит, кясилмязлик кими фундаментал анлайышлара ясасланыр. Диференсиал вя интеграл щесабынын инкишафы иля бу анлайышлар юз мцасир шяклини алмышдыр.

Тутаг ки, мадди нюгтя Ой оху б йунъа щярякят едир, х ися щяр щансы башланьыъ андан щесабланан замандыр. Щяр бир х заман анына щярякят едян нюгтянин й координатыны гаршы гойан й=ф(х) функсийасы бу щярякятин тясвирини верир. Бу функсийа механикада щярякят гануну адланыр. Щярякятин ясас характеристикасы (хцсусиля о мцнтязям дейился) щярякят едян нюгтянин заманын щяр бир х анындакы сцрятидир (бу сцряти щям дя ани сцрят адландырырлар). Яэяр нюгтя Ой оху бойунъа й=ф(х) гануну иля щярякят едирся, онда заманын ихтийари х анында о, ф(х) координатына, х+Δ х заман анында ися ф(х+Δх) координатына малик олур, бурада Δх – заманын артымыдыр. Щярякят едян нюгтянин х-дян х+Δх-я гядяр олан заман ярзиндя эетдийи йолу тясвир едян

                                        Δй =ф (х+Δ х) – ф(х)

ядяди функсийанын артымы адланыр.

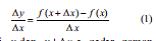
нисбяти х-дян х + Δ х-я гядяр заман мцддятиндя щярякят едян нюгтянин орта сцрятини ифадя едир. Δх сыфра йахынлашдыгда щярякят едян нюгтянин х заман мцддятиндяки (1) орта сцрятинин лимити ани сцрят (вя йа садяъя сцрят) адланыр, йяни

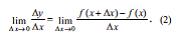
Ани сцрят анлайышы тюрямя анлайышына эятирир. Верилмиш гейд олунан х нюгтясиндя ихтийари й = ф(х) функсийасынын тюрямяси (2) лимитидир (о шяртля ки, бу лимит вар). й=ф(х) функсийанын верилмиш х нюгтясиндяки тюрямяси ф ′ (х), й′ , й, дф/дх, дй/дх, Дф(х) символларындан бири иля ишаря олунур. Тюрямянин тапылмасы ямялиййатына диференсиаллама дейилир.

Охй Декарт координат системиндя й =ф (х) тянлийи иля тяйин олунан мцстяви яйринин щяр щансы М(х, й) нюгтясиндя тохунанынын гурулмасы мясяляси дя (2) лимитиня эятирир (шякил). х аргументиня Δх артымыны вермякля вя яйри цзяриндя (х+Δх, ф(х+Δх)) координатлы М′ нюгтясини эютцряряк, М′ -и М-я йахынлашдырмагла тохунаны ММ′ кясянинин лимит вязиййяти кими тяйин едирляр (Δх сыфра йахынлашыр). Тохунанын кечдийи М нюг- тяси верилдийиндян, тохунанын гурулмасы онун буъаг ямсалынын (йяни онун Ох охуна мейил буъаьынын танэенсинин) тяйин олунмасына эятириб чыхарыр. Ох охуна паралел олан МП дцз хяттини чякмякля 

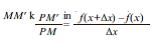
нисбятиня бярабяр олдуьу алыныр.

Яэяр й = ф(х) функсийасы х нюгтяси иля йанашы, щям дя онун щяр щансы ятрафында тяйин олунубса вя х нюгтясиндя тюрямяси варса, онда бу функсийа х нюгтясиндя кясилмяздир. Тярси доьру дейил, мяс., х=0 нюгтясинин истянилян ятрафында тяйин олунмуш, бу нюгтядя кясилмяз олан, лакин тюрямяси олмайан й = | х | функсийасы эюстярир ки, функсийанын верилмиш нюгтядя кясилмязлийиндян онун бу нюгтядя тюрямясинин олмасы алынмыр. Бундан ялавя юз тяйин областынын щяр бир нюгтясиндя кясилмяз олан, лакин бу тяйин областынын щеч бир нюгтясиндя тюрямяси олмайан функсийалар мювъуддур.

й = ф ( х ) функсийасы х нюгтясиндян йалныз саьда вя йа йалныз солда тяйин олундуьу щалда бу функсийанын х нюгтясиндя саь вя сол тюрямяси анлайышы дахил едилир. й = ф(х) функсийасынын х нюгтясиндя саь тюрямяси Δх мцсбят олмагла сыфра йахынлашдыгда (2) лимити кими тяйин олунур, сол
тюрямяси ися Δх мянфи олмагла сыфра йахынлашдыгда (2) лимити кими тяйин олунур. й = ф ( х ) функсийасынын х нюгтясиндя йалныз вя йалныз о вахт тюрямяси вар ки, онун бу нюгтядя бир-бириня бярабяр олан щям саь, щям дя сол тюрямяси олсун. Йухарыда верилян й = |х| функсийасынын х = 0
нюгтясиндя саь тюрямяси 1-я, сол тюрямяси -1-я бярабярдир, саь вя сол тюрямяляр бир-бириня бярабяр олмадыьына эюря бу функсийанын х = 0 нюгтясиндя тюрямяси йохдур. Тюрямяси олан функсийалар синифиндя диференсиаллама ямяли хяттидир, йяни

                                        ( ф (х)+э(х))′ = ф′ (х)+э′ (х)

вя истянилян α ядяди цчцн (αф(х))′ = αф ′ (х). Бундан ялавя ашаьыдакы диференсиаллама гайдалары доьрудур:

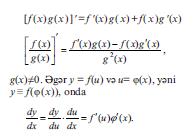
 Бязи елементар функсийаларын тюрямяляри:

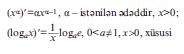
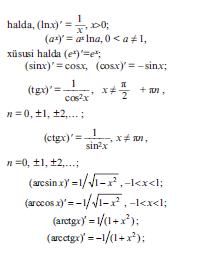
Истянилян елементар функсийанын тюрямяси дя елементар функсийадыр. Яэяр ф′ (х) тюрямясинин дя юз нювбясиндя верилян х нюгтясиндя тюрямяси варса, онда ф′ (х) функсийасынын тюрямясини й = ф(х) функсийасынын икинъи тяртиб тюрямяси адландырырлар вя ф ″(х), й″, й¨, д²ф/дх², д²й/дх², Д²ф(х) символларындан бири иля ишаря едирляр. Ой оху бойунъа й = ф(х) гануну цзря щярякят едян мадди нюгтя цчцн икинъи тяртиб тюрямя бу нюгтянин х заман анындакы тяъилини ифадя едир. Аналожи олараг ф^н(х), й(^н), д^нф /дх^н, д^нй/дх^н, Д^нф(х) символлары иля ишаря олунан истянилян н тяртибли тюрямя тяйин едилир.

Диференсиал. Яэяр аргументин Δх артымына й = ф(х) функсийасынын артымы уйьун эялирся, онда тяйин областы х нюгтясинин щяр щансы ятрафыны сахлайан й = ф(х) функсийасы х нюгтясиндя диференсиалланан функсийа адланыр, йяни Δй=ф(х+Δх)– ф(х) кямиййятини Δй=АΔх+αΔх кими ифадя етмяк олар, бурада А=А(х), Δх→0 олдугда α=α(х, Δх)→0 олур. Беляликля, АΔх ифадяси ф(х) функсийасынын х нюгтясиндяки диференсиалы адланыр, дй вя йа дф(х) символу иля ишаря едилир. Щяндяси олараг гейд олунмуш х гиймятиндя Δх артымы иля дяйишян диференсиал – тохунанын ординатынын артымыдыр, йяни ПМ″ парчасы (шякил). дй диференсиалы щям х нюгтясинин, щям дя Δх артымынын функсийасыдыр. Диференсиалы функсийанын артымынын хятти баш щиссяси адландырырлар, беля ки, х-ын гейд олунмуш гиймятиндя дй кямиййяти Δх-дан асылы хятти функсийадыр, Δй – дй фярги ися Δх→0 олдугда Δх-я нязярян сонсуз кичикдир. ф (х) ≡х функсийасы цчцн дх=Δх, йяни асылы олмайан дяйишянин дх диференсиалы онун Δх артымы иля цст-цстя дцшцр.

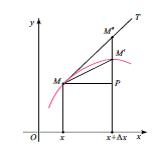
Бу, диференсиал цчцн ифадяни дй =Адх шяклиндя йазмаьа имкан верир.

Бирдяйишянли функсийа цчцн диференсиал анлайышы тюрямя анлайышы иля сых ялагялидир: й=ф (х) функсийасынын х нюгтясиндя диференсиалынын варлыьы цчцн зярури вя кафи шярт онун бу нюгтядя сонлу ф′ (х) тюрямясинин олмасыдыр, бу щалда дй= ф′ (х)дх бярабярлийи доьрудур. дй=ф′ (х)дх бярабярлийиня эюря диференсиалларын тапылмасы гайдасы билаваситя тюрямяляр цчцн уйьун тапылма гайдасындан чыхыр. Икинъи вя даща йцксяк тяртибли диференсиаллара да бахылыр.

Д.щ.-нын методлары бязи чохдяйишянли функсийаларын тядгигиндя дя истифадя олунур. й-ин гейд олунмуш гиймятиндя (й-я сабит кими бахмагла) М(х,й) нюгтясиндя у=ф(х,й) икидяйишянли функсийасынын х-я эюря тюрямяси – бу функсийанын х-я эюряхцсуси тюрямяси адланыр вя

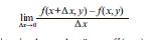
кими тяйин олунур, бу тюрямя f ′x (x, y), u′x ,∂u/∂x вя йа ∂f (x, y)/∂x кими ишаря олунур. у=ф(х,й) функсийасынын й-я эюря тюрямяси дя бу гайда иля тяйин едилир. Аналожи олараг йцксяк тяртибли хцсуси тюрямяляр дя тяйин олунур. Диференсиаллама заманы ейни дяйишяня эюря алынан ∂2 f /∂x2, ∂2 f /∂y2 тюрямяляри тямиз тюрямяляр, мцхтялиф дяйишяня эюря алынан ∂2 f /∂x∂y вя ∂2 f /∂y∂x тюрямяляри ися гарышыг тюрямяляр адланыр. Яэяр гарышыг тюрямяляр щяр бир нюгтядя кясилмяздирся, онлар бир-бириня бярабярдир. Бу тяриф вя ишарялямяляр даща чох дяйишяни олан функсийалар цчцн дя истифадя олунур.

Δу = ф(х+Δх,й+Δй) – ф(х,й) кямиййятиу функсийанын М(х,й) нюгтясиндя там артымы адланыр. Яэяр бу кямиййяти

шяклиндя эюстярмяк мцмкцндцрся (бурада А вя Б Δх вя Δй-дян асылы дейил, олдугда ися α сыфра йахынлашыр), онда у = ф(х,й) функсийасы М(х,й) нюгтясиндя диференсиалланан функсийа адланыр. АΔх +БΔй ъяминя у = ф(х,й) функсийасынын М(х,й) нюгтясиндя там диференсиалы дейилир вя ду кими ишаря олунур. Δх вя Δй артымларыны ися дх вя дй диференсиалларына бярабяр эютцрмяк олар, онда ду там диференсиалыны

шяклиндя йазмаг олар.

Щяндяси олараг у = ф(х,й) икидяйишянли функсийасынын верилмиш М(х,й) нюгтясиндя диференсиалланмасы бу нюгтядя онун графикиня тохунан мцстявинин олмасыдыр, бу функсийанын диференсиалы ися тохунан мцс- тявинин нюгтясинин аппликатынын артымыны (бу артым асылы олмайан дх вя дй дяйишянляринин артымына уйьундур) ифадя едир.

Тарихи мялумат. Д.щ. мцстягил фянн кими 17-ъи ясрин 2-ъи йарысында формалашды. Илк дяфя И.Нйутон вя Г.В.Лейбнитс тюрямя вя диференсиал васитясиля хцсуси мясялялярин щяллинин мцмкцнлцйцнц эюстярдиляр, диференсиаллама вя интегралламанын гаршылыглы тярс ямялляр олдуьуну ифадя едяряк диференсиал вя интеграл щесабынын инкишаф тямялини гойдулар. О вахтдан етибарян Д.щ., интеграл щесабы иля сых ялагядя, онунла бирликдя рийази анализин ясас щиссясини тяшкил етмякля инкишаф етди. Д.щ.-нын даща сонракы инкишафы Б.Тейлор, Ж.Лагранж, Й. вя И.Бернулли, О.Коши, К.Гаусс, Л.Ейлер вя б.-нын тядгигатлары иля баьлыдыр.

Диференсиал вя интеграл щесабынын йарадылмасы рийазиййатын инкишафында йени дювр ачды, йени рийази фянлярин (сыралар нязяриййяси, диференсиал тянликляр, диференсиал щяндяся, вариасийа щесабы, функсионал анализ) йаранмасы иля нятиъялянди, рийазиййатын тябиятшцнаслыг вя техниканын мясяляляриня тятбигини ящямиййятли дяряъядя эенишляндирди.