ДИФЕРЕНСИАЛ ЩЯНДЯСЯ – щяндясянин щяндяси обйектляри рийази анализ методлары, илк нювбядя диференсиал щесабы методлары иля юйрянян бюлмяси. Д.щ.-нин ясас обйектляри Евклид фязасынын яйриляри (дцз хятляри), сятщляри, щямчинин яйриляр вя сятщляр аиляляридир (кясилмяз чохлуглар). Бунунла беля, яйриляри, сятщляри вя йа онларын хцсуси синифлярини айрылыгда юйрянян елементар вя аналитик щяндясядян фяргли олараг, Д.щ.-дя цмумиййятля, башлыъа олараг еля яйриляря вя сятщляря бахылыр ки, онлары рийази анализ методларынын кюмяйиля арашдырылан тянликлярля ифадя етмяк мцмкцн олсун.

Д.щ.-дя бахылан яйриляр юзцнцн бязи хцсуси нюгтяляриндян башга бцтцн нюгтяляриндя тохунана малик олур. Яйрини кифайят гядяр щамар фярз етсяк, яйринин М′нюгтясиндян МТ тохунанына М нюгтясиндя чякилян М′М″ перпендикулйарынын уз. (шякил 1) сонсуз кичик кямиййят олар,

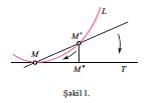
ММ″ парчасынын уз. иля мцгайисядя кичиклийин дяряъяси икинъинин дяряъясиндян кичик дейил (йяни М′ нюгтяси М-я йахынлашдыгда М′М″/( ММ″)² нисбяти мящдуд галыр). Яйринин МТ тохунанындан йайынма юлчцсц яйринин М нюгтясиндяки к яйрилийидир, к = 2лим М′М″/( ММ″)², бурада лимит М′ нюгтяси М-я йахынлашдыгда эютцрцлцр. Яйрилийя щямчинин яйринин истигамятинин дяйишмя сцряти кими дя бахмаг олар. Яэяр М вя М′ нюгтяляриндяки тохунанлар арасындакы буъаьы α иля (шякил 2) вя

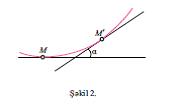
ММ′ гювсцнцн уз.-ну Δс иля ишаря етсяк, онда k = lim α/Δс. Бязи шяртляр дахилиндя мцстяви яйriniн яйрилийи гаршысында мцсбят вя йа мянфи ишаряляри йазырлар. Хцсуси щалда яэяр хятт дцз хятдирся, онун истигамяти бцтцн нюгтялярдя ейнидир, она эюря дя истянилян ММ′ парчасы цчцн α = 0 олур, демяли, к = 0, йяни дцз хяттин бцтцн нюгтялярдя яйрилийи сыфра бярабярдир. Диэяр бир хцсуси щалда, хятт – чеврядирся, онда буъаг ММ′ гювсцнцн мяркязи буъаьына бярабярдир, она эюря Δс = αР (Р – чеврянин радиусудур, бах шякил 3) вя

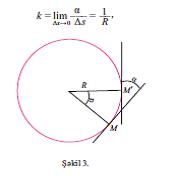
йяни чеврянин яйрилийи бцтцн нюгтялярдя ейнидир вя радиусун тярс гиймятиня бярабярдир. Ихтийари хятт щалында мцхтялиф нюгтялярдяки яйрилик, цмумиййятля, фярглидир. Мяс., шякил 4-дя тясвир олунмуш хяттин Г нюгтясиндяки яйрилийи М нюгтясиндяки яйриликдян даща чохдур.

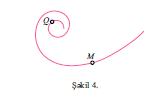
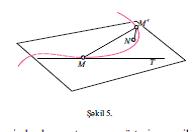
Фяза яйрилярини юйряняркян яйриликдян ялавя буруглуг (бурулма) анлайышы дахил едилир. Яэяр яйри бцтювлцкдя бир мцстяви цзяриндя йерляшмирся, онда онун чохтохунан мцстявиляри нюгтядян нюгтяйя кечдикдя дяйишир; бу дяйишиклик ня гядяр кяскин оларса, яйри бир о гядяр бюйцк буруглуьа малик олур. Буругларын сайы ашаьыдакы кими тяйин олунур. Тутаг ки, дяйишян нюгтя яйри цзря М нюгтясиндян М′ нюгтясиня кечир (шякил 5). Дяйишян нюгтядя чохтохунан мцстяви М нюгтя синдя олан чохтохунан мцстявийя мейил буъаьыны (сыфырдан башлайараг) дяйишир вя М′ нюгтясиндя йерляшяряк онунла щяр щансы β буъаьы ямяля эятирир (яэяр нюгтянин йердяйишмяси кичик оларса, β кичик ити буъаг олар). Яэяр мцшащидячи М-дян М′-я бахдыгда дяйишян чохтохунан мцстявинин саат ягряби истигамятиндя фырландыьыны эюрцрся, онда β буъаьы гаршысына мцсбят ишаря, якс щалда, мянфи ишаря йазылыр. β/Δс нисбяти (Δс – ММ′ гювсцнцн уз.-дур) ММ′ щиссясиндя яйринин буруглуьунун орта юлчцсц кими гябул едилир. Δс→0 олдугда, бу нисбятин лимити М нюгтясиндя σ буруглуьу адланыр. Хцсуси щалда яйри мцстяви яйриси олдугда, онун буруглуьу бцтцн нюгтялярдя сыфра бярабярдир; тярсиня, яэяр бцтцн нюгтялярдя буруглуг сыфра бярабярдирся, онда яйри бцтювлцкдя онун бцтцн нюгтяляри цчцн чохтохунан олан бир мцстяви цзяриндя йерляшир.

Д.щ. яйринин тохунаныны, яйрилийини вя буруглуьуну тапмаг цчцн цмуми цсуллар верир. Бу щалда яйри щяр щансы координат системиндя мцяййян тянликлярля верилмиш яйри щесаб олунур, дцзбуъаглы координат системиндя чох вахт

                                                  х = φ(у), й = ψ(у), з = χ(у) (1)

параметрик тянликляри иля верилир. Бурада у – мцяййян сонлу вя йа сонсуз интервалда гиймятляр алан сярбяст дяйишян (параметр адланыр), φ(у), ψ(у), χ(у) – верилмиш функсийалар, х, й, з щяр щансы М нюгтясинин дцзбуъаглы координатларыдыр. у-нун дяйишмяси иля х, й, з кямиййятляри дяйишир, бу ися М нюгтясинин йерини дяйишмяси демякдир. М нюгтясинин трайекторийасы (1) тянликляри иля верилян яйрини ифадя едир. Мяс., х = а ъосу, й =асину, з = бу, а > 0, б ≠ 0 тянликляри винтвары хятти тяйин едир: у артдыгъа М нюгтяси Оз оху ятрафында фырланыр вя ейни заманда бу ох бойунъа йерини дяйишир. (1) тянликляринин саь тяряфляриня М нюгтясинин р радиусвекторунун координат оху цзяриндяки пройексийасы кими бахмаг олар, бу беля йазылыр:

                                                      р=(φ(у), ψ(у), χ(у)).

φ′(у), ψ′(у), χ′(у) пройексийалы вектор р векторунун тюрямяси адланыр вя

иля ишаря олунур. Аналожи олараг йцксяк тяртибли тюрямяляр тяйин олунур:

Яйринин яйрилийи вя буруглуьу ону характеризя едян кямиййятлярдир. Яйрилик вя буруглуг ашаьыдакы дцстурларла щесабланыр:

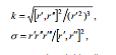
бурада [р′, р″] – вектроиал щасил, r′ r″ r′′′ ися гарышыг щасилдир. Бу щалда координат охлары системинин саь ориентасийайа малик олдуьу фярз едилир. Яйрилик вя буруглуг параметрин дяйишмясиня нязярян диференсиал инвариантдыр. Бу о демякдир ки, онлар р векторунун вя у параметринин диференсиаллары васитясиля ифадя олунур вя у = у(υ) дцстуру цзря йени υ параметриня кечдикдя онларын ифадяляри дяйишмир (йяни инвариантдыр).

Д.щ.-дя сятщ, адятян, цч тянликля тяйин олунур:

х = φ(у, υ), й = ψ(у, υ), з = χ(у, υ), (3) бурада у, υ параметр адланан асылы олмайан дяйишянляр, х, й, з ися щяр щансы М нюгтясинин дцзбуъаглы координатларыдыр. Фярз едилир ки, у вя υ параметрляри дцзбуъаглы координат системи дахил едилмиш кюмякчи мцстявинин щяр щансы Д областында гиймят алыр (дяйишир). Д областындан олан у вя υ-нин бцтцн мцмкцн гиймятляриндя М нюгтяси (3) тянликляри иля тяйин олунан сятщ цзяриндя йерляшир. Адятян, фярз едилир ки, у вя υ-нин бцтцн бахылан гиймятляриндя φ(у, υ), ψ(у, υ), χ(у, υ) функсийалары кясилмяздир вя ян азы 3-ъц тяртибя гядяр хцсуси тюрямяляри вар. (3) тянлийинин щяр бир у, υ гиймятляр ъцтц цчцн М нюгтясинин сятщ цзяриндя мцяййян вязиййятини гурурлар. Яэяр йалныз υ кямиййяти гейд олунмушдурса, онда у дяйишдикдя М нюгтяси сятщ цзяриндя координат хятти адланан мцяййян хятт ъызыр. υ-нин мцхтялиф гиймятляриня мцхтялиф координат хятляри уйьун эялир; онлар бирликдя υ =ъонст координат хятляр аилясини ямяля эятирир. Аналожи олараг у=ъонст хятляр аиляси тяйин едилир. Щяр ики аиля координат шябякясини ямяля эятирир. Яэяр шябякя верилмишдирся, онда сятщин, параметрлярин ики у=у₀, υ=υ₀ гиймятляри иля тяйин олунан истянилян нюгтяси уйьун координат хятляринин кясишмяси кими, йяни сятщ цзяриндя щяр щансы гурманын кюмяйи иля, щяъмлянян фязайа мцраъият етмядян тапыла биляр. Буна эюря у вя υ щямчинин сятщин нюгтяляринин дахили вя йа
яйрихятли координатлары адланыр.

(3) параметрик тянликляриндян ялавя, сятщ Ф(х, й, з) = 0 шяклиндя олан бир тянликля, йяни координатлары бу тянлийи юдяйян нюгтяляр чохлуьу кими вериля биляр. Яэяр сятщин параметрик тянлийи верилибся, онда у вя υ параметрлярини бу тянликдян кянар етмякля х,й,з арасында эюстярилян шякилдя мцнасибят алыныр. Мяс., х=асинуъосυ, й=асинусинυ, з=аъосу, а >0 тянликляри мяркязи координат башланьыъында радиусу

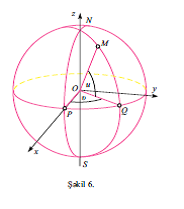
а олан сфера тяйин едир. Бу щалда, у, υ сферанын нюгтяляринин ъоьрафи координатлары адланыр (яэяр у, υ М нюгтясинин дахили координатларыдырса, онда у МОГ, υ ися ПОГ буъаьыдыр; шякил 6). υ = ъонст вя у = ъонст хятляри уйьун олараг сферанын меридианлары вя паралелляри адланыр (шякил 7). Бцтцн меридианларын бирляшдийи нюгтяляря ъоьрафи координатлар системинин гцтбляри дейилир (шякил 7-дя Н вя С нюг- тяляри). Сферанын верилмиш цч параметрик тянлийиндян у, υ параметрляринин кянар едилмяси х²+й²+з²=а² тянлийиня эятирир.

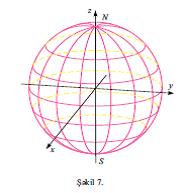
Д.щ. илк нювбядя сятщин регулйар вя йа ади нюгтялярини юйрянир. Сятщин нюгтяси о вахт регулйар адланыр ки, онун ятрафына дахили координатлары еля дахил етмяк олсун ки, бу ятрафын щяр бир нюгтясиндян у=ъонст аилясинин бир хятти вя υ= ъонст аилясинин бир хятти кечсин (хятляр мцхтялиф истигамятлидир). Бу шяртляр дахилиндя координат системинин юзц дя регулйар координат системи адланыр. Мяс., сфера цзяриндяки ъоьрафи координат системи Н вя С гцтбляри истисна олмагла щяр йердя регулйардыр, лакин Н вя С нюгтяляри сферанын регулйар нюгтяляридир, беля ки, сфера цзяриндя бу нюгтялярдя регулйар олан диэяр ъоьрафи координат системини (йени гцтбляри олан) дахил етмяк олар. Сятщин регулйар олмайан нюгтяси сятщин хцсуси нюгтяси адланыр (шякил 8-дя хцсуси нюгтяси олан сятщ тясвир олунмушдур). Сонралар дахили координатларын йалныз регулйар нюгтяляриня вя регулйар системляриня бахылаъаг.

Тутаг ки, щяр щансы сятщ (3) тянликляри иля верилмишдир. Онун х,й,з координатлы ихтийари М нюгтясинин р радиус-вектору у вя υ-дян асылы функсийа кими бу тянликлярля тяйин олунур. ру вя рυ хцсуси тюрямяляри М нюгтясиндян кечян υ= ъонст вя у= ъонст координат хятляринин тохунанлары истига- мятиндя йюнялян векторлардыр. Регулйар нюгтя вя регулйар координат системи ща-лында р_у вя р_в векторлары коллениар дейил.Она эюря дя М нюгтясиндян кечян вя р_у вя р_υ векторларыны сахлайан бир мцстяви вар. Бу мцстяви, сятщ цзяриндя М нюгтясиндян кечян щяр бир хяття чякилян тохунаны сахлайыр. Бу, М нюгтясиндя сятщя тохунан мцстяви адланыр. М нюгтясиндян кечян вя тохунан мцстявийя перпендикулйар олан (М нюгтясиндя) дцз хятт М нюгтясиндя сятщя чякилян нормал адланыр. Нормалын истигамяти [ р_у, р_υ] векториал щасили иля тяйин олунур.

Тутаг ки,

                           у = φ(т), υ = ψ(т) (4) 

тянликляри верилмишдир. Онда р вектору аргументляри у, υ олан т-дян асылы (аралыг) функсийадыр. т-нин дяйишмяси иля р векторунун сону верилмиш сятщ цзяриндя мцяййян хятт чякир; (4) тянликляри бу хяттин дахили тянликляри адланыр. Сятщляр нязяриййясинин ясас мясяляляриндян бири сятщ цзяриндяки хятляри онларын дахили тянликляри васитясиля арашдырмагдыр. Илк нювбядя хятлярин юлчцлмяси, йяни онун истянилян гювсцнцн уз.-нун щесабланмасына даир мясяля ортайа чыхыр.

Тутаг ки, с – сятщ цзяриндя хяттин гювсцнцн (у, υ дахили координатлары васитясиля сятщин щяр щансы гейд олунмуш нюгтясиндян ихтийари М нюгтясиня гядяр юлчцлян) уз.-дур. у=φ(т), υ=ψ(т) олдуьуна эюря с т параметриндян асылы функсийадыр; бу функсийанын диференсиалы

                                       дс² = дх²+дй²+дз² (5)

бярабярлийи иля тяйин олунур. Бу бяра бярabərлийин саь тяряфи др векторунун скалйар квад ратыдыр. др = р_уду+р_υдυ олдуьундан

                                      дс² = r ²_udu²+2р_ур_υдудυ+r²_υ dυ² (6)

олар. Бурада ду вя дυ верилмиш хяттин тянлийи иля тяйин олунур: ду=φ′(т)дт, дυ = ψ′(т)дт. Яксиня, r²_u, р_ур_υ вя r² υ ямсаллары сятщ цзяриндя кечирилян хятлярин неъя олма сындан асылы дейил, онлар сятщин юз тянлик ляри (3) иля тяйин олунур вя у вя υ-дян асылы функсийалардыр. r²_u =Е, р_u р _v=Ф, υ²_u=Э ишарялямясини дахил едяряк, (6) бярабярлийини 

                          dс²=Еду²+2Фдудυ+Эдυ² (7)

шяклиндя йазмаг олар. Саь тяряфдяки ифадя биринъи квадратик форма адланыр. Яэяр Е,Ф,Э мялумдурса, онда (4) хяттинин истянилян гювсцнцн
т-нин [т₁,т₂] парчасындакы дяйишмясиня уйьун олан уз.-ну

дцстуруна эюря щесабламаг олар. (7) квадратик формасы верилмиш сятщ цзяриндяки хятлярин гювсляринин уз.-ларыны щесабламаьа имкан верир, буна эюря дя ону сятщин метрик формасы адландырырлар. Бунунла бирликдя биринъи квадратик форма сятщин дахили щяндясясини, йяни щяъмлянян фязайа мцраъият етмядян сятщин юзцнцн цзяриндя апарылан юлчмялярин кюмяйиля алына билян фактлар йыьыныны тяйин едир. Сятщлярин дахили щяндясяси планиметрийанын эениш шякилдя цмумиляшдирилмясидир. Дахили щяндясядя истянилян сятщин дцз хятляри ролуну эеодезик хятляр ойнайыр. Ики сятщ о заман ейни дахили щяндясяйя малик олар ки, сятщлярдян бирини диэяриня еля гаршылыглы биргиймятли иникас етдирмяк мцмкцн олсун ки, эеодезик хятляр эеодезик хятляря кечсин вя онларын уз.-лары сахлансын. Беля сятщляр изометрик сятщляр адланыр.
Сятщин, онун дахили щяндясясинин дяйишмяз галдыьы кясилмяз деформасийа- сына сятщин яйилмяси
дейилир.

Д.щ. сятщлярин йалныз дахили хассялярини юйрянмякля кифайятлянмир. Сятщин фяза фигуру кими юйрянилмяси сятщ цзяриндя йерляшян хятлярин яйрилийиня бахмагла ясасландырылмышдыр. Тутаг ки, М (3) тянликляри иля тяйин олунан сятщин ихтийари нюгтяси, Н ися М нюгтясиндя нормалын ващид  векторудур (адятян, Н векторунун нормал цзря [р_у , р_υ] векториал щасилинин истигамятляндийи тяряфя доьру йюнялдийи фярз едилир). Яэяр М нюгтясиндя нормалдан, верилмиш др = р_уду+р_υдυ вектору истигамятиндя мцстяви кечирсяк, о, сятщи мцяййян хятт цзря кясяъяк. Хяттин чюкцклцйцнцн истигамяти Н векторунун иситигамяти иля цст-цстя дцшдцкдя хяттин М нюгтясиндя мцсбят ишаря иля, якс щалда ися мянфи ишаря иля эютцрцлян яйрилийи М нюгтясиндя сятщин др вектору истигамятиндя нормал яйрилийи адланыр. Нормал яйрилик 1/Р иля ишаря олунур вя бу дцстурла тяйин едилир:

бурада Щ = р_ууН, К = р_уυН, Л = р_υυН, дс² ися (7) дцстуру иля тяйин олунур.

                        Щду²+2Кдудυ+Лдυ² 

диференсиал квадратик формасына сятщин икинъи квадратик формасы дейилир. Сятщин нормал яйрилийи (онун щяр щансы М нюгтясиндя) др векторунун истигамятиндян асылыдыр. Нормал яйрилийин екстремал гиймятляр алдыьы истигамятляр М нюгтясиндя сятщин баш истигамятляри адланыр. Нормал яйрилийин сыфра чеврилдийи истигамятляр асимптотик истигамятляр адланыр.

Сятщлярин арашдырылмасы методлары онун щяр бир нюгтясинин йахын ятрафында йахшы ишлянмишдир. Онлар ясасян ашаьыдакы мцддяайа ясасланыр: сятщин дахили координатларла верилмиш щяр щансы ики квадратик формасы сятщи бярк ъисим кими тяйин едир (йяни сятщин йерляшмя дягиглийи иля). Тутаг ки,  Еду²+2Фдудυ+Ъдυ² вя Щду²+2Кдудυ+Лдυ² формалары верилмишдир, онда [Еду²+2Фдудυ+Ъдυ² формасынын мцсбят олмасы вя Щ, К, Л функсийаларынын щяр щансы цчтянликли системи юдямяси шярти дахилиндя] еля сятщ тапмаг олар ки, онлар щямин сятщ цчцн 1-ъи вя 2-ъи квадратик формалар олар.

Д.щ.-дя чох вахт айры-айры сятщ вя яйрилярля дейил, яйрилярин вя сятщлярин сонсуз аиляляри иля ишлямяк лазым эялир. Тутаг ки, х, й, з координатлары вя Ъ1,Ъ2, …, Ън ихтийари сабитляр дахил олан тянликляр верилмишдир, беля ки, бу сабитляр щяр дяфя щяр щансы ядяди гиймят алдыгда верилмиш тянликляр мцяййян бир яйрини (вя йа сятщи) тяйин едир. Ъ₁,Ъ₂, …, Ъ_н -нин бцтцн мцмкцн гиймятляриндя верилмиш тянликлярля тяйин олунан бцтцн яйриляр (вя йа сятщляр) чохлуьу н параметрли яйриляр (вя йа сятщляр) аиляси адланыр. Бурада фярз едилир ки, щямин чохлуг даща аз сайда ихтийари сабитлярля тяйин едиля билмяз.

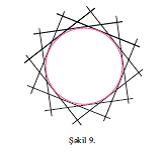
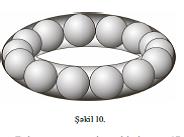
Бирпараметрли яйриляр, щямчинин бир вя ики параметрли сятщляр аилясинин юйрянилмясиндя гуршайан анлайышы бюйцк рол ойнайыр. Бирпараметрли яйриляр аилясинин гуршайаны юзцнцн щяр бир нюгтясиндя аилянин щяр щансы яйрисиня тохунан яйридир. Мяс., мцстяви цзяриндя верилмиш нюгтядян а мясафядя йерляшян дцз хятляр аилясинин гуршайаны мяркязи верилмиш нюгтядя олан, а радиуслу чеврядир (шякил 9). Щяр щансы сферанын ону кясмяйян ох ятрафында фырланмасындан алынан бирпараметрли сфералар аилясинин гуршайаны тордур (шякил 10).

Д.щ.-йя айрыъа анлайыш кими артыг 17 ясрин 2-ъи йарысында И.Нйутон, Г.В.Лейб- нитс, Х.Щцйэенс, Й. вя И.Бернуллинин ишляриндя раст эялинмишдир. 18 ясрин сонунда Л.Ейлерин вя Г.Монжун ишляринин кюмяйи иля сятщляр нязяриййясинин ясасы гойулмушдур. К.Гауссун эеодезийа вя картографийа мясяляляри Д.щ. цчцн хцсуси ящямиййят кясб едир. Сятщлярин ясас классик нязяриййясинин гурулмасы 1853 илдя бу нязяриййянин там тянликляр системини вермиш К.М.Петерсон тяряфиндян йекунлашдырылмышдыр. 19 ясрин 2-ъи йарысында сятщлярин классик нязяриййяси сащясиндя дярин вя цмуми нятиъяляр Ф.Миндиг, Ж.Лиувилл, Е.Белтрами, Ж.Г.Дарбу, Н.И.Лобачевски вя б. тяряфиндян алынмышдыр.