ДИФЕРЕНСИАЛЛАНМАЙАН ФУНКСИЙА – бирдяйишянли функсийа щалында тюрямяси олмайан функсийа. Мяс., ф (х)= | х | функсийасы х=0 нюгтясиндя диференсиалланмайан функсийадыр. Бунунла йанашы, функсийа саьдан вя солдан диференсиалланандыр, йяни бу нюгтядя саь вя сол тюрямяси вар. х≠0 вя ф (0)=0 олдугда кясилмяз олан

функсийасы х=0 нюгтясиндя няинки диференсиалланмайандыр, щям дя бу нюгтядя саь вя сол тюрямяляри (ня сонлу, ня дя сонсуз) йохдур.

Бцтцн ядяд охунда кясилмяз олан бцтцн нюгтялярдя сонлу тюрямяси олмайан функсийайа аид илк мисаллары Б.Болсано (1830) вя К.Вейерштрасс (1872) эюстярмишдир. Вейерштрасс функсийасы

сырасы иля верилир, бурада 0 < а < 1, б – тяк натурал ядяддир, аб >1+3π/2. ъосωх типли периодик функсийанын периодик сыныг хятлярля явяз едилмяси идейасы ясасында нисбятян садя мисал Б.Л. ван дер Варден тяряфиндян гурулмушдур. Тутаг ки, у0(х) – щяр бир щягиги х цчцн х вя она йахын
олан там ядядин фяргинин модулуна бярабяр олан функсийадыр. Бу функсийа [n/2, (n+1)/2] шяклиндя олан бцтцн парчаларда хятти функсийадыр, бурада н – там ядяддир: бу функсийа кясилмяздир вя ващидя бярабяр олан периода маликдир. Тутаг ки,

uk(x) = u0(4kx)/4k, к=1, 2,…

онда, ван дер Варден функсийасы

бярабярлийи иля верилир. Бу функсийа бцтцн ядяд охунда кясилмяздир вя щеч бир нюгтядя тюрямяси йохдур. Чохдяйишянли функсийа цчцн нюгтядя диференсиалланма бу нюгтядя хцсуси тюрямялярин олмасына еквивалент дейил. Хцсуси тюрямяляри олан диференсиалланмайан функсийалар мювъуддур. Мяс.,

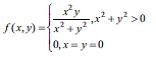
функсийасы мцстявинин бцтцн нюгтяляриндя кясилмяздир вя хцсуси тюрямяляри вар, лакин (0, 0) нюгтясиндя диференсиалланмыр.