ДИНАМИК СИСТЕМ – реал системин (физики, биоложи, игтисади вя с.) еволйусийасынын рийази модели; заманын истянилян анында онун вязиййяти башланьыъ вязиййяти иля мцяййян олунур.

Д.с. нязяриййясинин баниляри – А.Пуанкаре вя А.М.Лйапунов олмушдур. 19 ясрин сону, 20 ясрин яввялляриндя онлар ади диференсиал тянликляр системинин тякъя бир х(т) щяллиня дейил, реал (мяс., физики) системин мцхтялиф башланьыъ вязиййятляриня уйьун бцтцн щялляринин билинмяси ваъиб олан мясяляляр синфини дя арашдырмыш вя мцяййян етмишдиляр. Бу щалда х(т)-ни фязада бцтцн мцмкцн щалларын яйриси кими тясвир етмяк вя х(т) щяллинин баша дцшцлмяси вя тясвири цчцн бу яйринин щяндяси хассяляриндян истифадя етмяк олар.

Д.с.-я т заманы ярзиндя системин х₀ башланьыъ вязиййятиндян хт вязиййятиня кечмясини шяртляндирян {х} вязиййятляри фязасы вя т заманындан асылы олан φт еволйусийа оператору дахилдир. Д.с.-ин вязиййятини мцлащизялярин интерпретасийасынын, йазылышын, симметрийанын садялийиня эюря х дяйишянляр дясти иля тясвир едирляр. Д.с.-ин щяр бир вязиййятя бир нюгтя уйьун олан вязиййятляр чохлуьу онун фаза фязасыны ямяля эятирир, еволйусийа ися фаза фязасына дахил едилмиш нюгтянин фаза трайекторийасы – яйри бойунъа щярякяти иля тясвир едилир. Мяс., фаза фязасында ъазибя гцввясинин тясири иля щярякят едян н зярряъик, зярряъиклярин бцтцн координат вя сцрятляр дясти иля тясвир олунур, еволйусийа оператору ися уйьун биръинс диференсиал тянликляр системинин щялли иля мцяййян едилир.

Д.с.-и кясилмяз вя дискрет системляря айырмаг олар. Д.с. щямчинин x· =f (x) адибиръинс диференсиал тянликляр системи иля верилир, бурада щяр бир башланьыъ нюгтя цчцн х-ин йеэаня щялли вар. Беля Д.с.-ин х₀ – таразлыг вязиййяти _ф(х0_{) = 0} тянлийиндян тяйин олунур. О – таразлыг вязиййяти ятрафында юзцнц неъя апармасы йахынлыгдакы О системинин хяттиляшдирилмясинин хассяляриндян, даща дягиг, 

                                                   det ⎣∂f_i / ∂x_j – λδ_ij ⎦_x=_x0 = 0

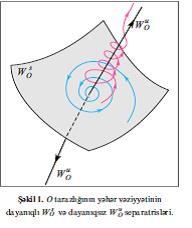
характеристик тянлийинин λ₁, λ₂, …, λ_н кюкляриндян асылыдыр, бурада δ_иж – Кронекер символудур. Тутаг ки, Реλ_ж п сайда кюкляр цчцн мянфи вя г сайда кюкляр цчцн мцсбятдир, беля ки, п+г = н. Яэяр п=н (г=н) оларса, онда О нюгтяси дайаныглы (дайаныгсыз) дцйцн адланыр. Фаза фязасында бу нюгтяйя йахын трайекторийалар дайаныглы дцйцн щалында т→ + ∞ олдугда, дайаныгсыз дцйцн щалында ися т→–∞ олдугда она йахынлашыр. Яэяр п≠г, г≠0 оларса, онда О нюгтяси йящяр адланыр. Ондан ики сятщ кечир: п-юлчцлц W^s₀ вя г-юлчцлц W^u₀– (бунлар О йящяринин дайаныглы вя дайаныгсыз чохобразлылары, щямчинин дайаныглы вя дайаныгсыз сепаратрисляр адланыр). Бу сятщляр О-йа уйьун олараг т→+∞ вя т→–∞ олдугда йахынлашан трайекторийалар тяряфиндян йарадылыр. Галан трайекторийалар йящярдян т→ ± ∞ олдугда узаглашыр  (шякил 1). Ейни заманда W^s₀  вя W^u₀-да йерляшян трайекторийалар (вя О иля цст-цстя дцшмяйян) щомоклиник трайекторийалар вя йа йящярин сепаратрисинин илэяйи адланыр. Кясилмяз мцщитин биръинс моделляриндя щомоклиник трайекторийалара солитон формасында гачан дальа уйьун олур.

x· =f (x) системинин периодик х = п (т) щялли ашаьыдакы хассяляря маликдир: истянилян т цчцн п (т) = п (т+Т ), бурада Т – периоддур. Бу щялля фаза фязасында Л гапалы трайекторийасы уйьун эялир. Л периодик трайекторийаларынын ятрафындакы трайекторийаларын юзцнц неъя апармасы, цзяриндя системин щялляринин хяттиляшдирил- мясинин кюмяйиля тапылан γ₁, γ₂,…, γ_н мултипликаторлары иля характеризя олунур. Онлардан бири γ_н– щямишя 1-я бярабярдир. Яэяр бцтцн н –1-ляр цчцн |γ_и| < 1 (|γ_и|> 1) оларса, онда Л трайекторийасы дайаныглыдыр (дайаныгсыздыр). Яэяр комлекс мцстявидя п
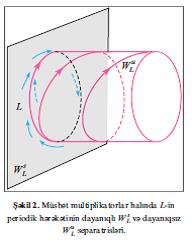
мултипликаторлары ващид даирянин дахилиндя, г мултипликаторлары ися хариъиндя йерляшярся, п+г = н –1, онда Л – йящяр типли трайекторийадыр. О ики (п+1)-юлчцлц W^s_L вя (г+1)-юлчцлц W^u_L сятщляринин кясишмясиндя йерляшир (дайаныглы вя дайаныгсыз сепаратрис). W^s_L (W^u_L)  – дайаныглы сятщи 
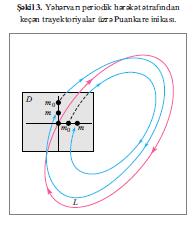
т→ + ∞ (т→ – ∞) олдугда, Л-я йахынлашан трайекторийалардан ибарятдир. н=3 вя п=г=1 олдугда, γ мултипликатору мцсбят вя 1-дян бюйцкдцрся, онда  сятщи W^s_L (W^u_L)   тоположи олараг силиндря еквивалентдир (шякил 2). Л ятрафында трайекторийанын юзцнц неъя апармасы Л-и кясян вя она йахын трайекторийада (н–1)-юлчцлц Д сятщи цзяриндя онларын изиня бахмагла юйрянилир. Яэяр Д цзяриндя олан м₀ нюгтяси Л-я кифайят гядяр йахындырса, онда м₀ нюгтясиндян кечян трайекторийа Д-ни диэяр ардыъыллыьын иникасы (Пуанкаре иникасы) адланан м нюгтясиндя кясир (шякил 3). Пуанкаре иникасынын Л иля Д-нин кясишмя нюгтясиндя хяттиляшдирилмяси Йакоби матриси иля тясвир олунур. Онун γ₁,…, γ_н–1 мяхсуси гиймятляри Л гапалы трайекторийасынын мултипликаторларыдыр. Периодик трайекторийаларын дайаныглы вя дайаныгсыз чохобразлылары кясишя билярляр. W^s_L вя  - W^u_L нун кясишмясиндян алынан вя Л-дян фяргли олан трайекторийайа щомоклиник трайекторийалар дейилир. Яэяр кясишмя тохунма олмадан баш верирся, онда щомоклиник трайекторийалар ятрафында мцхтялиф дайаныгсыз трайекторийалар мювъуддур, бунлар арасында сонсуз сайда йящяр типли гапалы трайекторийалар чохлуьу вар. Аналожи трайекторийалар чохлуьу хаотик динамикалы Д.с. цчцн дя доьрудур. Беляликля, щомоклиник трайекторийалар Д.с.-дя хаотик шяраитин олмасы критериси кими чыхыш едя биляр (бах Динамик хаос).

Дискрет заманлы Д.с. адятян Э фаза фязасынын юз-юзцня иникасы иля верилир: х_н+1 = Э(х_н). Онда φт (т = м) еволйусийа оператору Э-нин м дяфя алынмыш иникасы дыр: φнх = Э(Э(…Э(Х )…)).

Яслиндя Пуанкаре иникасы дискрет заманлы системи мцяййян едир. Мяс.,x· =f (x,θ) (θ· = ω, ф – θ вектор-функсийасына нязярян периодикдир) биръинс диференсиал тянликляр системи иля йазылан, периодик щяйяъанланманын системя тясирини тясвир едян Д.с. щяр заман Пуанкаре иникасыны доьурур. Беля системляр цчцн θ= 0 Пуанкаре сятщи мювъуддур ки, щяр бир трайекторийа бу сятщи сонсуз сайда кясир.

Д.с.-нин ваъиб щиссяляриндян бири – трайекторийаларын статистик хассялярини тясвир едян ергодик нязяриййядир. Яэяр онлар дайаныгсыздырса, онда башланьыъ вязиййятлярин йахын олмасына бахмайараг, еволйусийа просесиндя мцхтялиф трайекторийалар цзяриндя олан нюгтяляр бир-бириндян ящямиййятли дяряъядя узаглашыр, систем башланьыъ шяртляря “щисс едиляъяк” асылылыг нцмайиш етдирир.

Д.с. нязяриййясинин кюмяйиля динамик хаос, периодик вя хаотик рягслярин синхронлашмасы, диссипатив структурларын йарадылмасы, пайланмыш систем моделляриндя фяза-заман хаосу кими бир чох гейри-хятти тябият вя техника щадисяляри юйрянилмиш вя изащ едилмишдир.