ДИСПЕРСИЙА АНАЛИЗИ – рийазиййатда айры-айры факторларын експериментин нятиъясиня тясирини яввялъядян тяйин етмяк, щямчинин нювбяти експериментлярин планлашдырылмасы цчцн статистик метод.

Яэяр а₁, …, а_Ы мяъщул сабитляринин гиймятляри мцхтялиф методлар, йахуд М₁,…, М_ж юлчц васитяляриля юлчцля билярся вя биж систематик сящви, щям сечилмиш М_ж методундан, щям дя аинин юлчцлян мяъщул гиймятляриндян асылыдырса, онда беля юлчмялярин нятиъяляри

                  х_ижк=а_и+б_иж+й_ижк,

                   и=1,…, Ы, ж=1,…, Ж, к=1,…, К 

ъями шяклиндя тясвир едилир. Бурада К – а_и мяъщул кямиййятинин М_ж методу иля асылы олмайан юлчмяляринин сайы, йижк ися аи кямиййятинин М_ж методу иля к-нынъы юлчцлмясиндяки тясадцфи сящвдир. Щям дя фярз олунур ки, бцтцн й_ижк-лар – рийази эюзлямяси сыфыр олан, бярабяр пайланан асылы олмайан тясадцфи кямиййятлярдир. Беля хятти модел Д.а.-нин икифакторлу схеми адланыр. Биринъи фактор – юлчцлян кямиййятин щягиги гиймяти, икинъи юлчцлмя методудур, беля ки, бу щалда биринъи вя икинъи факторларын гиймятляринин щяр бир мцмкцн комбинасийасында ейни бир К сайда асылы олмайан юлчмяляр апарылыр (Д.а.-нин даща мцряккяб моделляриндя бязян сонунъу фярзиййядян имтина едирляр).

Мяс., тутаг ки, йарышда Ы сайда идманчы иштирак едир, онларын усталыьы Ж сайда щакимляр тяряфиндян гиймятляндирилир вя щяр бир иштиракчы К дяфя чыхыш етмялидир (К сайда ъящди вар). Бу щалда а_и – _и нюмряли идманчынын усталыьынын эюстяриъисинин щягиги гиймятидир, б_иж –ж нюмряли щакимин и нюмряли идманчынын усталыьына вердийи гиймятя дахил етдийи систематик сящвдир, х_ижк – к-ынъы ъящддя и нюмряли идманчыйа ж нюмряли щакимин вердийи гиймятдир, й_ижк– ися тясадцфи хятадыр. Фярз едяк ки,

                           ъ_иж = а_и + би_ж

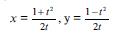
Тутаг ки, щямчинин 

α= ъ** , β_и = ъ_и* – ъ_** , γ_ж = ъ_*ж – ъ_**    вя δ_иж = ъ_иж – ъ_и* – ъ_*ж + ъ_** .

Д.а.-нин идейасы 

 ъ_иж = α + β_и + γ_ж + δ_иж , и =1,…, Ы, ж =1,…, Ж

бярабярликляриня ясасланыр. Идман йарышлары иля баьлы мисалда δ_иж – ж-ъи щакимин и-ъи идманчыйа мцнасибятини якс етдирир. Бцтцн δ_иж -лярин сыфыра бярабяр олмасы експертляр групунун иш цчцн иряли сцрдцйц ади тялябдир. Яэяр бу щипотез доьрудурса, онда ян йахшы зяминлярин мейдана чыхмасы вя ишлянмяси тяк-тяк щяйата кечириля биляр ки, бу да експериментлярин сайынын ящямиййятли дяряъядя азалмасына эятирир.

α, β_и, γ_ж вя δ_иж функсийаларынын щягиги гиймятляри мяъщулдур вя ъ_иж мяъщул функсийасы иля ифадя олунурлар. Она эюря дя Д.а.-нин биринъи мярщяляси х_ижк мцшащидяляринин нятиъяляриня ясасян ъ_иж цчцн статистик гиймятлярин ахтарылмасындан ибарятдир. Минимал дисперсийайа малик олан α, β_и, γ_ж, δ_иж функсийалары цчцн мейилсиз  aгиймятляри ъ_ij  аргументляринин уйьун ъ^{^}_иж гиймятляри иля явяз едилмяси нятиъясиндя алыныр.

Бу гиймятляндирмяляр ясасында Д.а.-нин биринъи вя икинъи факторларын експериментин нятиъяляриня тясиринин мейдана чыхмасыны билдирян икинъи мярщяляси гурулур. Статистик методларла  бярабярлийиня уйьун олан факторларын гаршылыглы тясиринин олмамасы щипотези, щямчинин  щипотезляриж i iйохланылыр. Нювбяти мярщялялярдя Д.а.тякъя реал конкрет мясялялярдян дейил, щям дя икинъи мярщялядя щипотезлярин статистик йохламаларынын нятиъяляриндян асылыдыр.

 Д.а. илк дяфя Р.Фишер тяряфиндян тяклиф едилмишдир (1925). Д.а. игтисадиййат, сосиолоэийа, биолоэийа вя техниканын бир сыра мясяляляриндя эениш тятбиг олунур. Бах, щямчинин Рийази статистика.