EVKLİD FƏZASI – 1) xassәlәri Evklid hәndәsәsinin aksiomları ilә tәsvir olunan fәza; 2) R hәqiqi әdәdlәr meydanı üzәrindә olan E vektor fәzası: bu fәzanın hәr bir x vә y vektorlar cütünә, uyğun hәqiqi әdәd [(x, y) – bu vektorların skalyar hasili adlanır] qarşı qoyulur. Skalyar hasil vasitәsilә E.f.-nda x vektorunun |x| uzunluğu, hәmçinin x vә y vektorları arasındakı (xy) bucağı tәyin olunur:
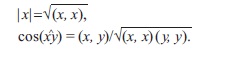
Bundan әlavә, ortoqonallıq anlayışı da daxil olunur: skalyar hasili sıfra bәrabәr olan vektorlar ortoqonal vektorlar hesab edilir.
E.f.-na aid misallar:
- Müstәvinin vә ya elementar Evklid hәndәsәsinin adi skalyar hasilli üçölçülü fәzasının bütün vektorları çoxluğu;
- R fәzası üzәrindә x = (x1, …, xn) vә y =( y1, ..., yn ) vektorlarının skalyar hasili
(x, y)= x1 y1+ …+ xn yn
kimi tәyin edilәn sonluölçülü vektor fәzası (n -ölçülü әdәdi Evklid fәzası). Eyniölçülü ixtiyari iki Evklid fәzası izomorfdur, yәni R üzәrindә olan, skalyar hasili saxlayan uyğun vektor fәzaların izomorfizmi mövcuddur. Adәtәn, sonsuz ölçülü E.f.-nı Hilbert fәzası adlandırırlar.














