ДЮВРИ ФУНКСИЙА – аргументинин гиймятляриня сыфырдан фяргли щяр щансы Т (бу, функсийанын дюврц адланыр) ядядини ялавя етдикдя гиймяти дяйишмяйян функсийа. Мяс., синх вя ъосх дюврц 2π олан Д.ф.-лардыр; тэх вя ътэх дюврц π олан Д.ф.-лардыр:

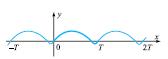
Е чохлуьунда тяйин олунмуш ф (х) функсийасы о вахт дюври функсийа олур ки, еля Т ≠ 0 ядяди олсун ки, истянилян х∈Е цчцн х + Т вя х–Т дя Е-йя дахил олсун вя ф (х ± Т )= ф (х) шярти юдянсин. Яэяр ф (х) функсийасы щяр щансы интервалда кясилмяздирся вя бу интервалда ф (х)≢ъонст оларса, онда бу функсийа цчцн ян кичик мцсбят Т дюврц мювъуддур; беляликля, бу функсийанын истянилян дюврц кТ шяклиндя олар, к = ±1, ±2, … .Т > 0 дюврлц Д.ф.-нын графикини гурмаг цчцн онун графикини [0, Т ] пaрчасында гурмаг кифайятдир, гурулмуш щиссяни абсис оху бойунъа ±Т, ±2Т, … гядяр сцрцшдцрмякля бцтцн график алыныр (шякил).

Ейни дюврлц функсийаларын ъями, фярги, щасили вя нисбяти дя щямин дюврлц Д.ф.-дыр. Д.ф.-нын тюрямяси дя щямин дюврлц Д.ф.-дыр. Яэяр Д.ф.-нын ибтидаи функсийасынын, узунлуьу дювря (периода) бярабяр олан парчада интегралы сыфра бярабярдирся, онда бу функсийа Д.ф. олур; бу щалда ибтидаи Д.ф. да щямин дюврлц Д.ф.-дыр.

Мцхтялиф дюврлц Д.ф.-ларын ъями йалныз вя йалныз онда Д.ф. олур ки, онларын дюврляри ортаг юлчцлц олсун. Мяс., син 2х + ъос3х 2π дюврлц Д.ф.-дыр; син х + синπх Д.ф. дейил: бу, санки дюври функсийайа мисалдыр.

Комплекс дяйишянли Д.ф.-лар комплекс дювря малик ола биляр. Мяс., ез Д.ф.-сы 2πи дюврлц, е ^(1+и)з Д.ф.-сы π (1+ и) дюврлц Д.ф.-лардыр. Кясилмяз Д.ф.-лар, нисбяти щягиги ядядя бярабяр олмайан ики Т₁ вя Т₂ дюврляриня малик ола биляр. Яэяр Т₁ вя Т₂ модулъа ян кичик дюврлярдирся, онда истянилян дювр к₁Т₁+к₂Т₂ шяклиндядир, к₁= 0, ±1, ±2, … , к₂= 0, ±1, ±2, … .Беля функсийалар икигат дюври функсийалар адланыр. Мяс., еллиптик функсийалар.