EYLER İNTEQRALLARI –

şәklindә (1-ci növ Eyler inteqralı vә ya 1730 –31-ci illәrdә L.Eyler tәrәfindәn öyrәnilәn beta-funksiya, әvvәllәr İ.Nyuton vә C.Vallis baxmışlar) vә

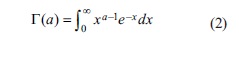
şәklindә inteqrallar [2-ci növ Eyler inteqralı vә ya 1729 –30-cu illәrdә L.Eyler tәrәfindәn (2) düsturuna ekvivalent olan formada baxılan  qamma-funksiya; (2) düsturuna L.Eylerin 1781 ildәki (1794 ildә nәşr olunub) işlәrindә rast gәlinir;  “E.i.” adı A.Lejandr tәrәfindәn verilmişdir]. E.i. Cⁿ_m – binomial әmsalları vә n! faktorial anlayışlarını ümumilәşdirmәyә imkan verir; belә ki, a vә b natural әdәd olduqda

axırıncı münasibәt beta-funksiyanı qamma-funksiyasına gәtirir. Arqumentin müxtәlif qiymәtlәrindә binomial әmsallar arasında uyğun  münasibәtlәri ümumilәşdirәn E.i. arasında bir sıra münasibәtlәr mövcuddur. E.i.-na a vә b-nin kompleks qiymәtlәrindә dә baxmaq olar. E.i.-na xüsusi funksiyalar nәzәriyyәsinin bir çox mәsәlәlәrindә rast gәlinir, elementar funksiyalarla ifadә olunmayan bir çox müәyyәn inteqrallar E.i.-na gәtirilir. F(a, b, c, x) hiperhәndәsi
funk siyasını ifadә edәn

inteqralı da E.i. adlanır.