EYNİGÜCLÜ TƏNLİKLƏR, e k v i v a l e n t t ә n l i k l ә r – köklәr (hәllәr) çoxluğu eyni olan tәnliklәr. Əgәr tәnliyin sağ vә sol tәrәfinә eyni bir analitik ifadәni (vә ya çoxhәdlini) әlavә etsәk vә ya hәr iki tәrәfi sıfırdan fәrqli eyni bir әdәdә vursaq, onda verilmiş tәnliklә eynigüclü olan tәnlik alarıq, mәs., x²– x+1=x–1 vә x²–2x + 2 = 0 tәnliklәri E.t.-dir (birinci tәnliyin hәr iki tәrәfinә x+1 çoxhәdlisi әlavә edilib); 0,01x²– 0 ,37x+1=0 vә x²–37x + 100 = 0 tәnliklәri dә E.t.-dir (birinci tәnliyin hәr iki tәrәfi 100-ә vurulub). Lakin tәnliyin hәr iki tәrәfini dәrәcәsi 1-dәn kiçik olmayan çoxhәdliyә vursaq vә ya bölsәk, alınan tәnlik, ümumiyyәtlә desәk, verilәn tәnliklә eynigüclü olmayacaq. Mәs., x–1=0 vә (x – 1)(x + 1) = 0 tәnliklәri E.t. deyildir (ikinci tәnliyin x = –1 kökü birinci tәnliyin kökü deyil). Verilmiş tәnliyin köklәri yerlәşәn meydan verildikdә E.t. anlayışı daha dәqiq ifadә olunur. Mәs., x²– 1=0 vә x⁴–1=0 tәnliklәri hәqiqi әdәdlәr meydanında E.t.-dir (hәr iki tәnlik üçün köklәr çoxluğu x₁=1, x₂=–1 әdәdlәrindәn ibarәtdir), lakin kompleks әdәdlәr meydanında bu tәnliklәr E.t. deyil, çünki ikinci tәnliyin әlavә iki xәyali kökü dә var: x₃= i, x₄= –i. E.t. anlayışı tәnliklәr sistemi üçün dә tәtbiq olunur. Hәllәr çoxluğu eyni olan iki sistem eynigüclü sis -
temlәr adlanır. İstәnilәn uyuşmayan tәnliklәr sistemi öz aralarında eyni güclüdür. Əgәr P(x, y) vә Q(x, y) – x, y dәyişәnlәrindәn asılı çoxhәdlilәrdirsә, a, b, c vә d isә әdәdlәrdirsә (hәqiqi vә ya kompleks), onda iki 

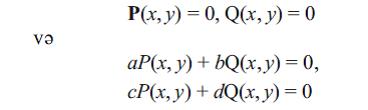
tәnliklәr sistemi ad – bc ≠ 0 (determinant) olduqda eynigüclüdür.