ДЦЗ ЩАСИЛ – чохлуглар нязяриййясинин ясас конструксийаларындан бири. Рийазиййатын бцтцн областларында эениш истифадя олунур. Термин илк дяфя Р.Декарт тяряфиндян аналитик щяндясянин гурулмасы заманы дахил едилмиш вя она эюря дя чох вахт Декарт щасили адланыр. Бязян “Д.щ.” явязиня, садяъя щ а с и л дя дейилир.
Ики А1 вя А2 чохлуьунун Д.щ.-и – бцтцн низамлы (а1, а2) ъцтляринин чохлуьудур, бурада а1∈А1, а2∈А2; щасил А1×А2 кими ишаря олунур. н >2 олдугда А1, А2, …, Ан чохлугларынын Д.щ.-и индуктив тяйин олунур:
А1 × А2 ×…× Ан = (А1× А2×…× Ан –1) × Ан.
О, (а1,а2,…,ан) шяклиндя бцтцн ардыъыллыглар чохлуьу иля ейниляшдириля биляр, бурада а1∈А1, а2∈А2, … , ан∈Ан. Бу ардыъыллыглар чох вахт н узунлуглу алай адландырылыр. н=1 олдугда щесаб едирляр ки, А1 чохлуьунун Д.щ.-и А1 иля цст-цстя дцшцр (тярифя ясасян), бош чохлуглар аилясинин Д.щ.-ини ися бирелементли чохлуьа бярабяр щесаб едирляр. Бош чохлуьун истянилян чохлугла Д.щ.-и бош чохлугдур.
Д.щ.-ин тярифиндя А1,…, Ан чохлуглары мцхтялиф щесаб едилмир. Бцтцн Аи =А олан Д.щ.-и ишаря етмяк цчцн Ан символундан истифадя олунур.
Яэяр П мцстявисиндя щяр щансы афин координат системи верилибся, онда мцстявинин нюгтяляри иля (х, й) низамланмыш щягиги ядядляр ъцтц арасында гаршылыглы бир- гиймятли уйьунлуг йарадылыр. Она эюря П мцстявисини Р2 (Р – щягиги ядядляр чохлуьудур) Декарт щасили иля, аналожи олараг цчюлчцлц фязаны Р3 иля ейниляшдирмяк олар. Яэяр П мцстявисиндя Охй координат системини вя уйьун олараг Ох вя Ой охунда [а, б] вя [с, д] парчаларыны айырсаг (шякил),
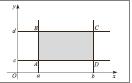
онда бу парчаларын Декарт щасилини тяпяляри А, Б, Ъ, Д олан дцзбуъаглы иля ейниляшдирмяк олар, бу нюгтялярин координатлары уйьун олараг (а, ъ), (а, д), (б, д), (б, ъ)-дир.
Яэяр А1 чохлуьунда м елемент, А2 чохлуьунда н елемент варса, онда онларын А1×А2 Д.щ.-и мн елементя маликдир (мяс., А21 м2 елементя, А31 м3 елементя маликдир вя с.). Бу мцнасибятляр “Д.щ.” термининин йаранмасыны изащ едир.
Сонсуз щал цчцн Д.щ.-ин гурулушу ашаьыдакы кими цмумиляшдирилир. Тутаг ки, Аи, и∈Ы вя Ы – там низамланмышдыр. Онда Аи, и∈Ы-лярин Д.щ.-и аи∈Аи олан бцтцн (а1, а2,…,аи,…) ардыъыллыгларындан тяшкил олунмушдур, бу, ∏ и∈Ы Аи символу иля ишаря олунур.
∏ и∈Ы Аи Д.щ.-и ашаьыдакы хассяляря маликдир: 1) щяр бир и∈Ы цчцн (а1,а2,…,аи,…) ардыъыллыьынын аи елементини гаршы гойан Пи : ∏и∈Ы Аи → Аи каноник иникасы вар. Бу иникас Д.щ.-ин Аи вуруьуна п р о й е к с и й а с ы адланыр; 2) ихтийари фи :Х → Аи иникаслар аиляси цчцн (Х щяр щансы чохлугдур, и∈Ы) еля йеэаня ф :Х → ∏ и∈Ы Аи иникасы мювъуддур ки, щяр бир и∈ Ы цчцн фПи =фи. Бу ики хасся Д.щ.-ин аксиоматик характеристикасыны верир, йяни Д.щ.-и биргиймятли тяйин едир.














