EHTİMAL NӘZӘRİYYӘSİ – tәsadüfi hadisәlәrin riyazi modellәrini öyrәnәn riyaziyyat bölmәsi. E.n. bir çox riyazi fәnlәrin, mәs., riyazi statistika, kütlәvi xidmәt nәzәriyyәsi, etibarlılıq nәzәryyәsi, maliyyә riyaziyyatının әsasını tәşkil edir.

Ehtimal nәzәriyyәsinin eksperimental әsasları. Tәsadüfi hadisә vә proseslәrin öyrәnilmәsi stasionar şәraitdә kütlәvi tәsadüfi hadisә vә proseslәrin tezliklәrinin statistik dayanıqlığı adlanan qanunauyğunluğa әsaslanır. Bu qanunauyğunluq eksperimental olaraq tәsdiqlәnmiş bir faktdır vә onun mahiyyәti aşağıdakı mülahizәlәrә әsaslanır: tutaq ki, A müәyyәn S şәrtlәr kompleksi ödәnilmәklә baş verә bilәn vә ya baş vermәyәn tәsadüfi hadisәdir. Әgәr S şәrtlәr kompleksi n dәfә ödәnilmәklә eksperimentlәr aparılırsa, onda deyilir ki, n sayda sınaq aparılmışdır. Tutaq ki, k_n(A) – A hadisәsinin n sınaqda başvermә sayıdir. k_n(A)/n nisbәtinә A hadisәsinin tezliyi deyilir. Sınaqların sayı n kifayәt qәdәr böyük olduqda, hadisәnin kn(A)/n tezliyi müәyyәn bir p (0 ≤ p ≤1) әdәdindәn çox az fәrqlәnir. Bu әdәd A hadisәsinin statistik ehtimalı adlanır vә P(A) ilә işarә olunur. Mәs., metal pulu n dәfә atdıqda “avers” üzü sınaqların tәxminәn yarısında düşür vә buna görә dә “avers” üzünün düşmәsi hadisәsinin ehtimalının 1/2-ә bәrabәr olduğu qәbul edilә bilәr. Statistika göstәrir ki, doğulan oğlan uşaqlarının sayı qızların sayından çoxdur vә doğulan uşaqların 51–52 faizini tәşkil edir, demәli, oğlan doğulması ehtimalı 1/2-dәn çoxdur.

Ehtimal nәzәriyyәsinin әsas anlayışları. Hәr bir sınaqda müşahidә oluna bilәn (mümkün) hadisәlәrdәn Ω yәqin hadisәsini vә ∅ qeyri-mümkün hadisәsini qeyd etmәk lazımdır. Ω hәr bir sınaqda hökmәn baş verәn hadisә, ∅ heç bir sınaqda baş vermәyәn hadisәdir. Müşahidә oluna bilәn A₁,…, A_r hadisәlәrinә әsaslanaraq, onların birlәşmәsi vә kәsişmәsi hadisәlәrini tәyin etmәk olur: yalnız vә yalnız A₁,…, A_r hadisәlәrindәn heç olmazsa biri baş verdikdә, baş verәn B hadisәsinә A₁,…, A_r hadisәlәrinin birlәşmәsi deyilir. Yalnız vә yalnız A₁,..., A_r hadisәlәrinin hamısı baş verdikdә, baş verәn C hadisәsinә A₁,…, A_r hadisәlәrinin kәsişmәsi deyilir. Hәr bir A hadisәsi üçün yalnız vә yalnız A hadisәsi –baş vermәdikdә baş verәn әks hadisәsi A daxil edilir. 

A₁,…, A_r hadisәlәrinin B birlәşmәsi simvolik olaraq 

kimi, kәsişmәsi isә

kimi (bәzәn dә C =A₁…A_r kimi) işarә edilir.

Urna sxemindә fәrz edilir ki, urnada hәr hansı sonlu Ω çoxluğunun ω elementlәri ilә işarә olunan kürәciklәr var. Qutudan tәsadüfәn bir ω kürәciyi çıxarılır. Әgәr ω∈A olarsa, onda deyilir ki, “A hadisәsi baş vermişdir”; A – Ω-nın qeyd olunmuş alt çoxluğudur. Belәliklә, bütün Ω çoxluğu yәqin hadisәyә (belә ki, ω ∈ Ω hәmişә ödәnilir), ∅ – boş çoxluğu isә qeyri-mümkün hadisәyә uyğundur (belә ki, ω∉∅ hәmişә doğrudur).

E.n.-ndә öyrәnilәn riyazi modellәrdә P(A) ehtimalı aksiomatik olaraq daxil edilir. Fәrz olunur ki, A hadisәlәri hәr hansı Ω={ω} elementar hadisәlәr fәzasının σ- cәbr tәşkil edәn alt çoxluqlar sinfi (yәni A sinfi ∅ vә Ω-nı özündә saxlayır, inkar әmәli, sonlu vә ya hesabi sayda birlәşmә, kәsişmә, iki hadisәnin fәrqi әmәllәrinә görә qapalı sinifdir) A-nın elementlәridir. P ehtimalı A∈A münasibәtini ödәyәn bütün hadisәlәr üçün tәyin olunmuşdur vә aşağıdakı aksiomları ödәyir:

A1. P(A) ≥ 0 (P-nin mәnfi olmaması)

A2. P(Ω)=1 (P-nin normalanmış olması)

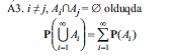
(P-nin hesabi additivliyi).

A-da tәyin olunmuş P ehtimalı A1, A2, A3 aksiomlarını ödәyәrsә, (Ω, A, P) üçlüyü ehtimal fәzası adlanır.

Bu aksiomatika 1933 ildә A.N. Kolmoqorov tәrәfindәn tәklif olunmuşdur vә hazırda E.n.-nin әsaslandırılması üçün әn geniş yayılmış mәntiqi sxem sayılır. Real tәsadüfi hadisәlәrin tezliklәri (nisbi tezliklәri) mәnfi olmamaq, normalanmış olmaq vә hesabi additivlik xassәlәrini ödәdiyindәn vә hadisәnin tezliyi ehtimala yaxın olduğundan, P(A) ehtimalının da bu xassәlәri ödәmәsi tәlәbi tәbiidir. P ehtimalının hesabi additiv olması tәlәbi tam riyazi nәzәriyyәnin yaradılması üçün zәruridir. Ehtimal fәzası qurularkәn P ehtimalını müxtәlif üsullarla vermәk olar. Mәs., Ω sonlu fәza olarsa, ehtimal fәzası da sonlu olur. Bu halda P ehtimalı aşağıdakı şәrtlәri ödәyәn p(ω), (ω∈ Ω) elementar ehtimalları vasitәsilә tәyin olunur:

A hadisәsinin P(A) ehtimalının qiymәti isә

ilә müәyyәn edilir. Elementar hadisәlәr bәrabәrimkanlı olduqda, bütün p(ω)-lar bir-birinә bәrabәr hesab edilir vә nәticәdә (1) ifadәsinin xüsusi halı olaraq ehtimalın klassik tәrifi alınır:

burada N(A) – A çoxluğunun elementlәrinin sayıdır, yәni A hadisәsinin ehtimalı A hadisәsi üçün әlverişli elementar hadisәlәr sayının bütün elementar hadisәlәr sayına nisbәtinә bәrabәrdir.

Digәr mühüm hal P ehtimalının bәrabәrimkanlılıq anlayışının ümumilәşdirilmәsi baxımından verilmәsidir. Tutaq ki, Ω – hәr hansı mәhdud Evklid fәzası, m(Ω) bu oblastın Lebeq ölçüsü olarsa (birölçülü vә ikiölçülü fәzalarda bu ölçü uyğun olaraq uzunluq vә sahәdir) vә ixtiyari ω∈ Ω nöqtәlәrinin hamısı “bәrabәrimkanlı” olarsa, onda hәr bir A∈ A çoxluğuna

ehtimalı qarşı qoyulur. Bu halda (2) düsturu ilә tәyin edilәn ehtimal hәndәsi ehtimal adlanır.

A1–A3 aksiomları ilә tәyin olunan P ehtimalı Ω-nın alt çoxluqlarından tәşkil olunmuş A σ-cәbrindә normalanmış ölçüdür. Bu halda E.n.-nә ölçü nәzәriyyәsinin hissәsi kimi baxmaq olardı, lakin E.n. vә ölçü nәzәriyyәsinin әsas problemlәri müxtәlifdir. E.n.-nin yalnız özünәmәxsus әsas spesifik anlayışı asılı olmamazlıq anlayışıdır.

A hadisәsinin B hadisәsinә nәzәrәn şәrti ehtimalı

                              P(A|B)= P(A∩B)/P(B), P(B) > 0                                     (3)

düsturu ilә tәyin olunur.

Әgәr                                   

                                P(A|B)=P(A)                                            (4)

olarsa, onda A hadisәsi B hadisәsindәn asılı olmayan (vә ya ehtimali asılı olmayan) hadisә adlanır. (3) vә (4)-dәn A vә B hadisәlәrinin asılı olmamazlıq şәrti (simmetriklik) alınır:

                                               P(A∩B) = P(A)P(B).                             (5)

Daha ümumi halda әgәr istәnilәn A_i∈ A_i hadisәlәri üçün (i = 1,…, r)

                                       P(A₁∩…∩A_r)=P(A₁)P(A₂)P(A_r)

şәrti ödәnilәrsә, A₁,…, A_r ⊂ A hadisәlәrinin σ-cәbrlәri asılı olmayan σ-cәbrlәr adlanır.

Asılı olmamazlıq anlayışı vә şәrti ehtimallar sınaqlarla әlaqәdar hallara baxılarkәn xüsusi әhәmiyyәt kәsb edir. Sadә hallarda sınaq müәyyәn şәrtlәr kompleksi ödәnilmәklә eksperimentdә, yalnız vә yalnız biri baş verә bilәcәk vә ya baş vermәyәcәk bütün mümkün ola bilәn cüt-cüt uyuşmayan {A_i} hadisәlәr çoxluğudur.

Bir çox hallarda sınaqların nәticәlәri hәr hansı әdәdi qiymәtlәrlә ifadә olunur, bu halda tәsadüfi kәmiyyәtdәn söhbәt gedir. Әgәr (Ω, A, P) ehtimal fәzası verilibsә, onda ξ = ξ(ω) tәsadüfi kәmiyyәti ω elementar hadisәsinin ölçülәn funksiyasıdır, yәni ξ(ω) elә funksiyadır ki, әgәr B ixtiyari Borel funksiyası olarsa, onda {ω: ξ(ω)∈B}∈A, yәni {ω: ξ(ω)∈B} tәsadüfi hadisәdir, B ⊂ R¹. {ω: ξ(ω)∈B} tәsadüfi kәmiyyәtinin Pξ(B) ehtimalı (B-nin funksiyası) ξ(ω) tәsadüfi kәmiyyәtinin paylanma qanunu adlanır.

Pξ(B) paylanma qanununu Fξ(x)=P{ω: ξ(ω ) < x}, х∈ (–∞, ∞) paylanma funksiyası vasitәsilә hәmişә tәyin etmәk olar.

Bir çox halda tәsadüfi kәmiyyәtin ehtimali paylanması әvәzinә onun әdәdi xarakteristikaları ilә kifayәtlәnmәk olur. Bunlardan әn çox istifadә olunanı riyazi gözlәmә vә dispersiya әdәdi xarakteristikalarıdır.

Bir neçә tәsadüfi kәmiyyәt eyni zamanda öyrәnildikdә birgә paylanma anlayışından istifadә olunur. Belә paylanma ξ₁,…, ξ_n tәsadüfi kәmiyyәtlәri üçün                  

ehtimalları ilә verilir; burada B – R¹-in Borel çoxluğudur, B∈ Rⁿ. İxtiyari seçilmiş B∈ R¹ Borel çoxluqları üçün

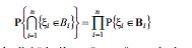
bәrabәrliyi ödәnilәrsә, ξ₁, …, ξ_n – asılı olmayan tәsadüfi kәmiyyәtlәr adlanır.

Limit teoremlәri. Tәsadüfi kәmiyyәtlәrin birgә paylanması vasitәsilә bu kәmiyyәtlәrlә tәyin edilәn istәnilәn hadisәnin [mәs., {а < ξ₁+…+ξ_n< b} hadisәsinin] ehtimalını hesablamaq olar. Qeyd etmәk lazımdır ki, yalnız limit teoremlәrini әhatә edәn biliyә malik olduqda E.n.-nin mahiyyәti dәrindәn dәrk olunur. Mәs., Bernulli teoremi onu ifadә edir ki, asılı olmayan sınaqlarda müşahidә oluna bilәn hәr hansı tәsadüfi hadisәnin tezliyi bir qayda olaraq, bu hadisәnin ehtimalından az fәrqlәnir, Muavr – Laplas teoremi isә bu vә ya digәr yayınmaların ehtimallarını qiymәtlәndirmәk üçün istifadә edilir. Analoji olaraq, tәsadüfi kәmiyyәtin riyazi gözlәmәsi vә dispersiyası kimi әdәdi xarakteristikalarının mәğzi böyük әdәdlәr qanunu vә mәrkәzi limit teoremi ilә aydın olur.

ξ¹,…,ξ_n,… – riyazi gözlәmәsi Мξk=a vә dispersiyası Dξ_k=σ² olan eyni qanunla paylanmış asılı olmayan tәsadüfi kәmiyyәtlәr,

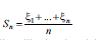
isә bu ardıcıllığın ilk n kәmiyyәtinin әdәdi ortası olsun. Böyük әdәdlәr qanununa görә ixtiyari ε > 0 qiymәtindә {|S_n – a| ≤ ε} hadisәsinin  ehtimalının limiti n → ∞ olduqda 1-ә bәrabәrdir vә belәliklә, bir qayda olaraq S_n a orta qiymәtindәn az fәrqlәnir. Mәrkәzi limit teoremi bu nәticәni dәqiqlәşdirir vә onu ifadә edir ki, S_n-in a- dan yayınmaları tәqribi olaraq riyazi gözlәmәsi 0, dispersiyası σ²/n olan normal paylanmaya tabedir.

Tәsadüfi proseslәr. Limit teoremlәrinin әksәriyyәtinin yaranma mexanizmi yalnız tәsadüfi proseslәr nәzәriyyәsi ilә bağlı tam mәnada dәrk olunur.

20 әsrin ortalarında bir sıra fiziki vә kimyәvi tәdqiqatlarla bağlı birölçülü vә çoxölçülü tәsadüfi kәmiyyәtlәrlә yanaşı, tәsadüfi proseslәr – zaman etibarı ilә cәrәyan edәn vә ehtimal qanunları ilә idarә olunan proseslәr öyrәnilmәyә başlandı. Tәsadüfi prosesә misal hissәciyin Broun
hәrәkәtidir. E.n.-dә tәsadüfi prosesә, ξ(t) birparametrli tәsadüfi kәmiyyәtlәr ailәsi kimi baxılır. Әksәr hallarda t parametri zamanı ifadә edir, lakin prosesin parametri, mәs., ixtiyari dәyişәn olduğu halda, tәsadüfi proses әvәzinә tәsadüfi funksiya, әgәr t fәza nöqtәsidirsә, tәsadüfi meydan termini işlәdilir. t tamqiymәtli olarsa, tәsadüfi funksiya tәsadüfi ardıcıllıq adlanır. Tәsadüfi kәmiyyәt paylanma qanunu ilә xarakterizә olunduğu kimi tәsadüfi proses sonluölçülü paylanmaları ilә ξ(t₁),ξ(t₂),…, ξ(t_n) tәsadüfi kәmiyyәtlәrinin birgә paylanmaları toplusu ilә xarakterizә oluna bilir; t₁, t₂, …, t_n n-nin ixtiyari qiymәti üçün mümkün zaman anlarıdır.

Tәsadüfi proseslәr nәzәriyyәsindә Markov proseslәri, stasionar tәsadüfi proseslәr, şaxәlәnәn proseslәr, hәmçinin martinqallar daha çox öyrәnilmişdir. Tәsadüfi proseslәr nәzәriyyәsi tәsadüfi kәmiyyәtlәr cәmi üçün limit teoremlәrinin klassik problemlәri ilә sıx bağlıdır. Tәsadüfi kәmiyyәtlәr cәminin paylanma qanunlarından alınan limit paylanmaları, tәsadüfi proseslәr nәzәriyyәsindә uyğun xarakteristikaların dәqiq paylanma qanunlarıdır. Bu fakt bir çox limit teoremlәrini uyğun tәsadüfi proseslәrin kömәyilә isbat etmәyә imkan yaradır.

Tarixi mәlumat. E.n. 17 әsrin ortalarında yaranmışdır. E.n.-ә aid ilk tәdqiqatlar B. Paskal, P. Ferma, X. Hüygensә aiddir vә müxtәlif azart oyunlarda müxtәlif tәsadüfi hadisәlәrin ehtimallarının hesablanması ilә bağlı aparılmışdır. Y. Bernullinin, iki nәticәli, asılı olmayan sınaqlar sxemi üçün böyük әdәdlәr qanununu isbat etmәsi, E.n.-dә mühüm әhәmiyyәt kәsb etdi (1713 ildә çap olunmuşdur).

E.n. tarixinin sonrakı (ikinci) mәrhәlәsi (18 әsr vә 19 әsrin başlanğıcı) A.Muavr, P. Laplas, K.Qauss vә S.Puasson kimi alimlәrin adları ilә bağlıdır. Bu dövrdә E.n. tәbiәtşünaslıq vә texnikada (әsasәn, mü- şahidәlәrin xәtaları nәzәriyyәsindә, geodeziya vә astronomiyada, atıcılıq nәzәriyyәsindә) xüsusilә aktual tәtbiqlәri ilә sәciyyәvidir.

Laplas (1812) vә Puasson (1837) teo- remlәri kimi mәlum olan ilkin limit teo- remlәri bu dövrә aiddir; elә bu әrәfәdә A. Lejandr vә K. Qauss (1808) әn kiçik kvadratlar üsulunu işlәmişlәr.

E.n.-nin üçüncü mәrhәlәsi (19 әsrin 2-ci yarısı) әsas etibarı ilә P.L. Çebışev, A.M. Lyapunov vә A.A. Markov kimi alimlәrin adları ilә bağlıdır. Onlar hәlli Bernulli vә Muavr–Laplas teoremlәrinin ümumilәşmәsinә gәtirәn bir sıra mәsәlәlәrin әsasını qoydular. Çebışev daha ümumi ehtimallar üçün böyük әdәdlәr qanununu isbat etdi (1867). İlk dәfә o, asılı olmayan tәsadüfi kәmiyyәtlәrin cәmi üçün mәrkәzi limit teoremini tәrtib etdi vә onun isbat edilmәsi üsullarından birini göstәrdi. Bu teoremin başqa bir isbat üsulunu A.M.Lyapunov tapdı (1901). A.A. Markov asılı sınaqların bir halına baxdı (1907) vә bu, sonradan Markov zәnciri adını aldı.

19 әsrin ikinci yarısında Qәrbi Avropada riyazi statistika (A. Ketle, F. Qalton) vә statistik fizikaya aid (L.Boltsman) araşdırmalar geniş surәtdә inkişaf etdi vә bu araşdırmalar P.L.Çebışev,  A.M.Lyapunov vә A.A.Markovun әsas işlәri ilә yanaşı, E.n.-nin problemlәrinin әsaslı tәdqiqatı üçün dördüncü (müasir) inkişaf mәrhәlәsinin әsasını qoydu. Bu mәrhәlә E.n.-nin geniş tәtbiqi ilә sәciyyәvidir. Bu dövrdә Fransada E.Borel, P.Levi, M.Freşe, Almaniyada R.Mizes, ABŞ-da N.Viner, V.Feller, C.Dub, İsveçdә Q.Kramer kimi alimlәrin faydalı araşdırmaları ilә yanaşı, S.N.Bernşteynin fәaliyyәti xüsusilә qeyd olunmalıdır. S.N.Bernşteynin fәaliyyәti ilә E.n.-nin yeni mәrhәlәsinin tәmәli qoyuldu. O, Çebışev, Lyapunov vә Markovun klassik limit teoremlәrini olduqca ümumilәşdirdi vә E.n.-nin tәbiәt elmlәrinә geniş tәtbiqi mәsәlәsini qoydu. A.Y.Xinçin vә A.N.Kolmoqorov E.n. mәsәlәlәrinә hәqiqi dәyişәnli funksiyalar nәzәriyyәsinin metodlarını tәtbiq etmәyә başladılar.