EKSTREMUM (lat. extremum – kәnar, sәrhәd) – f(x) kәsilmәz funksiyasının maksimumu vә ya minimumu olan qiymәt. Daha dәqiq, x0 nöqtәsindә kәsilmәz olan f (x) funksiyası üçün bu funksiyanın tәyin oblastından götürülmüş elә (x0 + δ, x0 – δ) әtrafı var ki, bu әtrafın bütün nöqtәlәrindә f (x0) ≥ f(x) [uyğun olaraq f (x0) ≤ f (x)] bәrabәrsizliyi ödәnir, onda x0 nöqtәsindә f (x) funksiyasının maksimumu (lokal maksimumu) vә ya minimumu (lokal mini- mumu) var.
Әgәr x ≠ x0 olduqda, elә әtraf varsa vә orada f (x0) > f (x) [vә ya f (x0) < f (x)] olsun, onda ciddi lokal maksimum (vә ya ciddi lokal minimum), әks halda qeyri-ciddi lokal maksimum (vә ya qeyri-ciddi lokal minimum) haqqında danışılır. 1-ci şәkildә A nöqtәsindә ciddi lokal maksimum, B nöqtәsindә qeyri-ciddi lokal minimum alınır.
Lokal maksimumdan fәrqli olaraq E çoxluğunda kәsilmәz olan funksiyanın maksimumuna (minimumuna) mütlәq maksimum (minimum) deyilir. Funksiyanın mütlәq maksimumu (minimumu) eyni zamanda hәm dә lokal maksimumdur (minimumdur), lakin funksiyanın lokal maksimumu (minimumu) mütlәq maksimumdan (minimumdan) kiçik (böyük) ola bilәr. Lokal maksimumu axtararkәn lokal maksimumlar (minimumlar) tapılır vә onların arasından әn böyüyü (kiçiyi) seçilir.
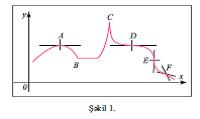
Maksimum vә minimum nöqtәlәrinә e k s t r e m u m n ö q t ә l ә r i deyilir. Funksiyanın hәr hansı x0 nöqtәsindә E.-u olması üçün bu funksiyanın x0 nöqtәsindә kәsilmәz olması vә ya f′(x0) = 0 olması zәruridir (şәkil 1-dә A nöqtәsi), әks halda f′(x)-in olmaması zәruridir (şәkil 1-dә C ). Әgәr x0 nöqtәsinin hәr hansı әtrafında f′(x) törәmәsi x0-dan solda müsbәt vә sağda mәnfidirsә, onda f′(x)-in x0 nöqtәsindә maksimumu var: әgәr f′(x) x0-dan solda mәnfi vә sağda müsbәtdirsә, onda x0-da minimumu var (birinci kafi şәrt). Әgәr x0 nöqtәsinә keçdikdә f′(x) işarәsini dәyişmirsә, onda f(x) funksiyasının x0 nöqtәsindә E.-u yoxdur (şәkil 1-dә D, E vә F nöqtәlәri). Әgәr x0 nöqtәsindә f(x)-in n ardıcıl törәmәsi varsa, hәm dә f′(x0) = f ″(x0) = … = f (n–1)(x0) = 0 vә f (n)(x0) ≠ 0-dırsa, tәk n-lәr üçün x0 nöqtәsindә f (x)-in E.-u yoxdur, cüt n-lәr üçün isә f (n)(x0) > 0 olduqda minimumu, f (n)(x0) < 0 olduqda isә maksimumu var. Funksiyanın E.-unu onun әn böyük vә әn kiçik qiymәtlәri ilә qarışdırmaq olmaz.
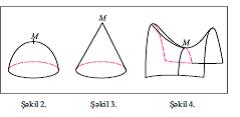
Birdәyişәnli funksiyanın E.-una ana- loji olaraq, çoxdәyişәnli funksiyanın E.-u müәyyәn olunur. Bu halda funksiyanın törәmәsinin sıfra bәrabәr olması vә ya 1-ci tәrtib xüsusi törәmәlәrinin mövcud olmaması zәruri şәrtdir. Mәs., şәkil 2-dә tәsvir olunan sәthlәrdә M nöqtәsindә xüsusi törәmәlәr sıfra bәrabәrdir, şәkil 3-dә M nöqtәsindә onlar mövcud deyil. Әgәr M (x0, y0) nöqtәsinin hәr hansı әtrafında f (x, y) funksiyasının 1-ci vә 2-ci tәrtib xüsusi törәmәlәri varsa vә kәsilmәzdirlәrsә, hәmçinin hәmin nöqtәdә,
![]()
olarsa, onda f (x, y) funksiyasının M nöqtәsindә E.-u var ( f"xx < 0 olduqda maksimumu vә f"xx > 0 olduqda minimumu); әgәr Δ < 0 olarsa, M nöqtәsindә E. yoxdur (bu halda M yәhәr nöqtәsi vә ya minimaks nöqtәsi adlanır, şәkil 4).
Çoxdәyişәnli funksiyanın E.-u üçün kafi şәrt kvadratik formanın müsbәt (vә ya mәnfi) olması ilә müәyyәn edilir:
![]()
burada aik – araşdırılan nöqtәdә fxixk′′ -nın qiymәtidir, bax hәmçinin Şәrti ekstremum. E. termini hәm dә variasiya hesabında funksionalların әn böyük vә әn kiçik qiymәtlәrinin öyrәnilmәsi zamanı tәtbiq edilir.














