ELASTİKLİK MODULU – cismin elastiklik xassәlәrini xarakterizә edәn kәmiyyәt; xüsusi halda Huk qanununun riyazi ifadәsindәki mütәnasiblik әmsalı. Deformasiyanın növlәrinә görә E.m. da müxtәlifdir. Mәs., u z u n u n a E.m. (yaxud Yunq modulu E); E = σ/ε, burada σ – normal gәrginlik, ε – bu gәrginliyin tәsiri istiqamәtindәki nisbi uzanmadır. Yunq modulu materialın dartılmaya müqavimәt qabiliyyәtini xarakterizә edir. E n i n ә  E.m. (yaxud sürüşmә modulu, G); G = τ/γ, burada τ – toxunan gәrginlik, γ – sürüşmә bucağıdır. Sürüşmә modulu material hәcmini saxladığı zaman öz formasının dәyişmәsinә müqavimәt qabiliyyәtini tәyin edir. H ә c m i  s ı x ı l m a modulu (K); K = σ /Δ, burada σ – normal gәrginlik, Δ – nisbi hәcmi sıxılmadır. Hәcmi E.m. material formasını saxlamaqla öz hәcminin dәyişmәsinә müqavimәt qabiliyyәtini xarakterizә edir. Materialın elastiklik xassәsini xarakterizә edәn sabit kәmiyyәtlәr sırasına hәmçinin Puasson әmsalı (ν) da aiddir: ν = │ε¹│/ε, burada ε¹ – kәsiyin nisbi eninә sıxılması (birtәrәfli dartılma zamanı), ε – nisbi uzanmadır.

Bircins izotrop cisim halında E.m. bütün istiqamәtlәr üzrә eynidir. Dörd E, G, K vә ν sabit kәmiyyәtlәr öz aralarında iki riyazi ifadә ilә әlaqәlidirlәr:

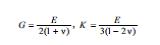
Demәli, onlardan yalnız ikisi sәrbәst kәmiyyәtdir vә izotrop cismin elastiklik xassәlәri iki elastiklik sabiti ilә tәyin edilir. Anizotrop material halında E, G vә ν müxtәlif istiqamәtlәrdә müxtәlif qiymәtlәr alır vә geniş çәrçivәdә dәyişә bilәrlәr. Anizotrop materialın E.m.-nun sayı materialın quruluşundan asılıdır. Elastiklik xassәlәrinә nәzәrәn heç bir simmetriyası olmayan anizotrop cisim 21 E.m.-na malikdir.
Simmetriya olduqda E.m.-nun sayı azalır.

E.m. öyrәnilәn materialların nümunәlәrinin eksperimental-mexaniki sınaqları ilә müәyyәn edilir. Eyni bir material üçün E.m. ciddi sabit kәmiyyәt olmayıb materialın kimyәvi tәrkibindәn, onun әlavә emalından asılı olaraq dәyişir. E.m.-nun qiymәtlәri materialın temp-rundan da asılıdır.