ELASTİKLİK NӘZӘRİYYӘSİ – mexanika bölmәsi; qüvvәlәrin tәsiri ilә sakit halda vә ya hәrәkәtdә olan elastik cisimlәrdә baş verәn yerdәyişmә, deformasiya vә gәrginliyi öyrәnir. E.n. tikintidә, maşınqayırmada, dağ-mәdәn işlәrindә, ümumiyyәtlә, texnika vә sәnayenin müxtәlif sahәlәrindә, hәmçinin fizikada, seysmologiyada, biomexanikada vә digәr elmlәrdә möhkәmliyә, formanın dәyişmәsinә vә dayanıqlığa aid hesablamaların nәzәri әsasıdır. E.n. metodları ilә qüvvәlәrin tәsiri altında olan müxtәlif cisimlәr (maşınlar, qurğular, konstruksiyalar vә onların elementlәri, bәndlәr, geoloji strukturlar, canlı orqanizmin hissәlәri vә s.) tәdqiq olunur vә hesablamalar nәticәsindә nәzәrdә tutulan obyektdә gәrginlik vә ya yerdәyişmә yaratmayan (yolverilәn) qüvvәlәr tәyin edilir.

Әksәr materiallar üçün elastiklik qa- nunları kiçik (bәzәn dә böyük) deformasiyalarda gәrginlik vә deformasiyaların ani qiymәtlәri arasında qarşılıqlı birqiymәtli asılılığı әks etdirir. E.n.-nin әsas qanunu– ümumilәşmiş Huk qanunudur. Bu qanuna görә gәrginliklәr deformasiyalardan xәtti asılıdır. İzotrop materiallar üçün bu asılılıqlar aşağıdakı kimidir:

σ₁₁ = 3λε + 2με₁₁, σ₂₂ = 3λε + 2με₂₂ ,
σ₃₃ = 3λε + 2με₃₃,                                                              (1)
σ₁₂ = 2με₁₂, σ₂₃= 2με₂₃, σ₃₁ = 2με₃₁,

burada   orta (hidrostatik) deformasiya, λ vә μ – Lame sabitlәridir. Belәliklә, izotrop materialın elastik xassәlәri iki λ vә μ sabitlәri ilә, yaxud bunlarla ifadә olunan iki elastiklik modulu ilә xarakterizә edilir. (1) bәrabәrliyini hәmçinin aşağıdakı şәkildә dә vermәk olar:

σ₁₁ – σ = 2μ (ε₁₁ – ε),…,
σ ₁₂ = 2με₁₂,…, σ = 3Kε, (2)

burada  orta (hidrostatik) gәrginlik, K – hәcmi elastiklik moduludur.

Qeyri-xәtti elastik izotrop material üçün (2) bәrabәrliklәrinә μ әvәzinә hәr yerdә Φ(ε_u)/3ε_u әmsalı daxil olur, σ = 3Kε ifadәsi isә σ = f (ε) bәrabәrliyi ilә әvәz olunur, burada εu deformasiyanın intensivliyi, Φ vә f funksiyaları isә verilәn material üçün universal olub tәcrübәlәrdәn tәyin edilir. Φ (εu) müәyyәn böhran qiymәtinә çatdıqda plastik deformasiya baş verir.

Tarazlıq zamanı, tәsir edәn qüvvәlәri vә sәrhәd şәrtlәrini bilmәklә, cismin istәnilәn nöqtәsindә gәrginlik vә deformasiyaların tenzorları komponentlәrinin qiymәtlәri, hәmçinin cismin hissәciyinin yerdәyişmә vektorunun u_x, u_y, u_z komponentlәri E.n. әsasında tәyin edilir. Bu mәsәlәnin hәlli üçün başlanğıcda tarazlığın diferensial tәnliklәri götürülür:

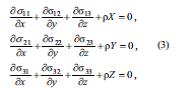
burada ρ – materialın sıxlığı, X, Y, Z – cismin hәr bir hissәciyinә tәsir edәn kütlә qüvvәsinin (mәs., ağırlıq qüvvәsinin) koordinat oxları üzәrindә proyeksiyalarıdır.

Cismin izotrop halında tarazlığın 3 tәnliyinә (1)-in 6 bәrabәrliyi, hәmçinin deformasiyalar vә yerdәyişmәlәr arasındakı asılılığı müәyyәnlәşdirәn aşağıdakı şәkildә daha 6 bәrabәrlik qoşulur:

Cismin sәrhәd sәthinin S₁ hissәsinә F_x, F_y, F_z proyeksiyaları vahid sәthә aid edilәn verilmiş sәth qüvvәlәri (mәs., kontakt qarşılıqlı tәsir qüvvәlәri) tәsir etdikdә, bu sәthin S₂ hissәsi üçün isә onun nöqtәlәrinin φ_x, φ_y, φ_z yerdәyişmәlәri verildikdә sәrhәd şәrtlәri aşağıdakı şәkildә olur:

σ₁₁l₁+ σ₁₂ l₂ + σ₁₃ l₃ = F_x,                            (5)
. . . . . . . . . .
. . . . . . . . . .
u_x= φ_x, u_y= φ_y, u_z = φ_z                                 , (6)

burada l₁, l₂, l₃ – koordinat oxları vә sәthin normalı arasındakı bucaqların kosinuslarıdır. Birinci şәrtlәr onu göstәrir ki, axtarılan gәrginliklәr S₁ sәrhәdindә (5)-in üç bәrabәrliyini, ikinci şәrtlәrdәn isә görü- nür ki, yerdәyişmәlәr S₂ sәrhәdindә (6) bәrabәrliklәrini ödәmәlidir; xüsusi halda φ _x=φ_y= φ_z= 0 ola bilәr (S₂ sәthinin bir hi sәsi möhkәm bәrkidilmişdir).

Termoelastiklik mәsәlәsindә cisimdә temp-run qeyri-bircins paylanması nәticәsindә әmәlә gәlәn gәrginlik vә deformasiya tәyin edilir. Bu mәsәlәnin riyazi qoyuluşu zamanı (1)-in ilk üç tәnliklәrinin sağ tәrәfinә (3λ + 2μ)α T hәddi әlavә olunur, burada α – istidәn xәtti genişlәnmә әmsalı, T(x₁, x₂, x₃) – verilәn temp-r sahәsidir. Analoji olaraq elektromaqnitoelastiklik vә şüalanmaya mәruz qalan cisimlәrin elastiklik nәzәriyyәsi qurulur.

E.n.-nin qeyri-bircins cisimlәr üçün olan mәsәlәlәri böyük praktiki әhәmiyyәtә malikdir. Bu mәsәlәlәrdә (1) tәnliklәrindәki λ vә μ әmsalları sabit olmayıb cismin elastik xassәlәrinin sahәsini müәyyәn edәn koordinatların funksiyalarıdır. Buna müvafiq olaraq E.n.-nin polikristal cisimlәrin xassәlәrinin statistik metodları işlәnib hazırlanır.

E.n.-nin dinamika mәsәlәlәrindә ax- tarılan kәmiyyәtlәr koordinatların vә zamanın funksiyalarıdır. Bu mәsәlәlәrin riyazi hәlli üçün (3) tәnliklәrindәn fәrqli olaraq başlanğıcda, sağ tәrәfindә hәrәkәtin sıfıra bәrabәr olmayan ρ∂²ux/∂t² vә s. olan tәnliklәri götürülür. Başlanğıc tәnliklәrә (1), (4) tәnliklәri vә (5), (6) sәrhәd şәrtlәrindәn başqa, mәs., başlanğıc zaman anında cismin zәrrәciklәrinin yerdәyişmәlәri vә sürәtlәrinin paylanmasını tәyin edәn ilkin şәrtlәr dә qoyulmalıdır. Bu tip mәsәlәlәrә konstruksiyalara vә qurğulara, hәmçinin elastik dalğaların
paylanmasına aid mәsәlәlәr daxildir.

E.n.-nin müasir problemlәrindәn biri mәsәlәlәrin riyazi qoyuluşu vә onların böyük elastik deformasiyalarda hәlli metodlarının işlәnib hazırlanmasıdır.

E.n.-nin eksperimental metodları tәdqiq olunan obyektdәki vә ya onun sәthindәki gәrginliklәri vә deformasiyaları bәzi hallarda bilavasitә tәyin etmәyә imkan verir. Bu metodlar hәm dә analitik vә hesablama metodları ilә, xüsusilә dә hәr hansı sadәlәşdirilmiş fәrziyyәlәrlә tapılan hәllәri yoxlamaq üçün istifadә edilir. Bәzәn axtarılan funksiyalara aid az qisim informasiyaları tәcrübәlәrdәn әldә edәn eksperimental-nәzәri metodlar effektiv olur.