ELEKTROMAQNİT SAHӘSİNİN POTENSİALLARI – elektromaqnit sahәsinin energetik xarakteristikaları. Elektrostatikada vektor elektrik sahәsini bir skalyar funksiya ilә – elektrostatik potensialla xarakterizә etmәk olur. Ümumi halda ixtiyari elektromaqnit sahәsinin tәsviri üçün iki vektor – maqnit induksiyası vektoru (B) vә elektrik sahәsinin intensivlik vektorunun (E) әvәzinә iki digәr kәmiyyәti: A(x, y, z, t) vektor potensialını vә φ (x, y, z, t) skalyar potensialını daxil etmәk olar (burada x, y, z– koordinatlar, t – zaman), hәm dә B vә E vektorları A vә φ ilә birqiymәtli ifadә olunur:

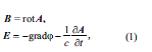
burada c – işığın vakuumda sürәtidir.

Sahәnin potensialları üçün tәnliklәr Maksvell tәnliklәrinә nisbәtәn daha sadә formaya malikdir ki, bu da dәyişәn elektromaqnit sahәlәrinin tapılması mәsәlәsini sadәlәşdirir. E.s.p. üçün tәnliklәrin әhәmiyyәtli dәrәcәdә sadәlәşmәsi ona görә mümkündür ki, potensiallar birqiymәtli
tәyin olunmur. Әgәr A vә φ-nin әvәzinә yeni potensiallar seçsәk 

burada χ – koordinat vә zamanın ixtiyari funksiyasıdır, onda (1) tәnliklәri ilә tәyin edilәn B vә E vektorları dәyişmәyәcәk. Potensialların çevrilmәlәrinә [(2)] görә elektromaqnit sahәsinin invariantlığı k a l i b r l ә n m  i ş  vә ya q r a d i y e  n t  i n v a r i a n  t l ı ğ ı adlanır. Kalibrlәnmiş invariantlıq E.s.p.-na әlavә şәrt qoymağa imkan verir. Belә әlavә şәrt әsasәn L o r e n s   ş ә r t i  d i r:

burada ε vә μ – mühitin dielektrik vә maqnit nüfuzluğudur. Bircins mühitdә (ε = const, μ = const) Maksvell tәnliklәrindәn E.s.p. üçün alınan tәnlik (3) şәrtlәrindәn istifadә edildikdә eyni formaya malik olur:

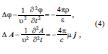
burada  Laplas operatoru, ρ vә j – yük vә cәrәyanın sıxlığı, elektromaqnit sahәsinin mühitdә yayılma sürәtidir. ρ = 0 vә j = 0 olarsa, E.s.p. dalğa tәnliyini ödәyir.

(4) tәnliklәri yüklәrin vә cәrәyanların mәlum paylanmasına görә A vә φ potensiallarını vә demәli, (1) düsturlarının kömәyi ilә elektromaqnit sahәsinin B vә E xarakteristikalarını tәyin etmәyә imkan verir.