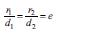ELLİPS (yun. ἒλλειψις – çatışmazlıq) – düz dairәvi konusu bu konusun tәpәsindәn keçmәyәn vә bütün doğuranları kәsәn müstәvi ilә kәsdikdә alınan en kәsik. E., hәmçinin müstәvinin müәyyәn F₁(– c, 0) vә F₂(c, 0) (bunlar E.-in fokusları adlanır) nöqtәlәrindәn r₁= F₁M vә r₂=F₂M mәsafәlәrinin cәmi sabit olan M nöqtәlәrinin çoxluğu (hәndәsi yeri) kimi tәyin olunur (şәkil): r₁+r₂= 2a. F₁F₂ parçasının (fokus

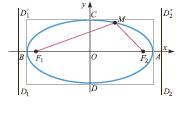
mәsafәsinin) O orta nöqtәsi ellipsin mәrkәzi adlanır. Başlanğıcı E.-in mәrkәzindә olan Oxy düzbucaqlı koordinat sistemindә fokusları Ox oxu üzәrindә olan ellipsin tәnliyi

kanonik şәklini alır. Burada a=OA=OB vә b=OC=OD E.-in böyük vә kiçik yarım- oxlarıdır; OF₁=OF₂=c. a=b olduqda F₁ vә F₂ fokusları üst-üstә düşür vә verilmiş tәnlik, E.-in xüsusi halı kimi baxılan çevrәni tәyin edir. E. ikitәrtibli mәrkәzi xәtdir. E. Ox vә Oy oxlarına (böyük vә kiçik oxlar) vә mәrkәzә nәzәrәn simmetrik olan qapalı xәtdir. E.-in forması ellipsin ekssentrisitetinin qiymәti ilә müәyyәn olunur: e=c/a nisbәtinә onun ekssentrisiteti deyilir (çevrә üçün e = 0). E.-in kiçik oxuna paralel olan vә onun mәrkәzindәn d=± a/e mәsafәdә olan D₁D₁′ vә D₂D_2^′ düz xәtlәri E.-in direktrislәri adlanır. Ellipsin ixtiyari nöqtәsindәn fokusa qәdәr olan mәsafәnin hәmin nöqtәdәn uyğun direktrisә qәdәr olan mәsafәyә nisbәti sabit kәmiyyәt olub, ekssentrisitetә bәrabәrdir: