ELLİPSOİD (lat. ellips vә yun. εδος –görünüş) – mәrkәzi ikitәrtibli qapalı sәth. Başlanğıcı E.-in simmetriya mәrkәzindә olan Oxyz düzbucaqlı koordinat sistemindә, koordinat oxları E.-in simmetriya oxları ilә, koordinat müstәvilәri isә E.-in simmetriya müstәvilәri ilә üst-üstә düşәn (şәkil 1) E.-in tәnliyi

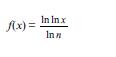
kanonik şәklini alır, burada a, b vә c (vә bu uzunluqda olan parçalar) e l l i p s o i d i n   y a r ı m o x l a r ı  adlanır.

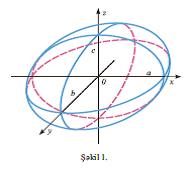
Әgәr a ≠ b ≠ c olarsa, E. ü ç o x l u e l l i p s o i d adlanır. Әgәr a = b > c-dirsә, onda E. s ı x ı l m ı ş  f ı r l a n m a  e l l i p s o i d i  vә ya sferoid adlanır: xOz müstәvisindә yerlәşәn  ellipsinin öz kiçik oxu әtrafında fırlanması nәticәsindә alınır (şәkil 2). Әgәr a > b = c 

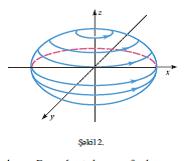
olarsa, E. – d a r t ı l m ı ş  f ı r l a n m a  e l l i p s  o i d i adlanır: ellipsin öz böyük oxu әtrafında fırlanmasından alınır (şәkil 3). Әgәr a = b = c olarsa, E. radiusu a olan x²+ y²+ z²= a² sferasıdır. Sferanı iki

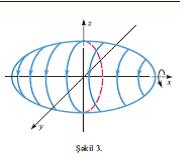
perpendikulyar müstәviyә nәzәrәn bәrabәr ölçüdә sıxmaqla üçoxlu E.-i almaq olar. E.-in bütün müstәvi kәsiklәri ellipslәrdir (xüsusi halda
çevrәlәrdir). E.-in hәcmi  kimi tapılır.