elliptik inteqralların çevrilmәsi ilә әlaqәli funksiyalar. E.f. riyaziyyatın vә mexanikanın bir çox sahәlәrindә nәzәri araşdırmalarda vә әdәdi hesablamalarda tәtbiq edilir.
u = sin x triqonometrik funksiyasının
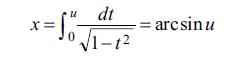
inteqralına nәzәrәn tәrs funksiya olmasına oxşar olaraq birinci növ normal
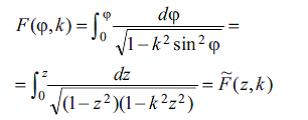
elliptik inteqralı (z = sin φ, k – elliptik inteqralın moduludur) φ = am z – z-in a m p l i t u d u n u (bu funksiya E.f. deyil) vә ω=sn z= sin(am z) – a m p l i t u d u n s i n u s u funksiyalarını әmәlә gәtirir. cn z – a m p l i t u d u n k o s i n u s u vә dn z – amplitudun deltası
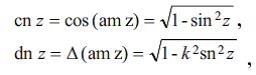
düsturları ilә tәyin olunur.
sn z, cn z, dn z funksiyalarını Y a k o b i E.f.-ı adlandırırlar, onlar
sn2z+cn2z = k2sn2z+dn2z=1
münasibәti ilә әlaqәlidir. Şәkildә hәqiqi x vә 0 < k < 1 üçün Yakobi E.f.-ının qrafiklәrinin forması tәsvir edilib.
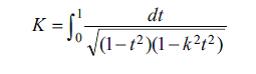
isә 1-ci növ tam normal elliptik tәnlikdir vә 4K – sn z E.f.-nın әsas dövrüdür. Birdövrlü sinx funksiyasından fәrqli olaraq sn z – ikidövrlüdür. Onun ikinci әsas dövrü 2iK′ә bәrabәrdir, burada
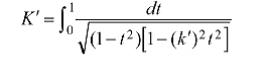
vә ![]() – ә l a v ә m o d u l d u r .
– ә l a v ә m o d u l d u r .
Yakobi E.f.-nın dövrlәri, sıfırları vә polyusları cәdvәldә verilmişdir, burada m vә n istәnilәn tam әdәdlәrdir.
℘(x) Veyerştrass E.f.-ı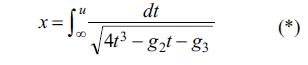
birinci növ normal elliptik Veyerştrass inteqralının tәrsi kimi müәyyәn oluna bilәr, burada g2 vә g3 – ℘(x)-in i n v a r i a n t l a r ı adlanır. Bununla bәrabәr, fәrz edilir ki, 4t3–g2t– g3 çoxhәdlisinin e1,e2 vә e3 sıfırları öz aralarında müxtәlifdir (әks halda (*) inteqralı elementar funksiyalarla ifadә olunardı).
℘(x) Veyerştrass E.f.-ı Yakobi E.f.-ı ilә aşağıdakı münasibәtlәrlә әlaqәlidir:
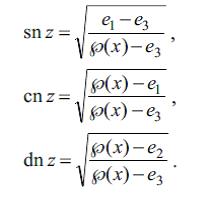
Nisbәtlәri xәyali әdәd olan ω1 vә ω2 dövrlü istәnilәn ikidövrlü meromorf funksiya [yәni m, n=0, ±1, ±2,… olduqda f(z+mω1+ nω2) = f(z) vә Im(ω1/ω2)≠0] E.f.-dır.
E.f.-ın, hәmçinin әdәdi hesablamaların qurulması üçün siqma-funksiyalar vә tetafunksiyalar tәtbiq olunur.
E.f. nәzәriyyәsinin әsas banilәri N.Abel (1822) vә K. Yakobidir (1829). Sonuncunun geniş şәkildә ifadә etdiyi E.f. nәzәriyyәsi onun adını daşıyır. 1847 ildә J. Liuvil ikidövrlü meramorf funksiyalar kimi baxılan ümumi E.f. nәzәriyyәsinin әsaslarının xülasәsini çap etdirmişdir. E.f.-ın ℘-funksiya, hәmçinin ξ-, σ-funksiya ilә ifadәsi K. Veyerştrass tәrәfindәn 19 әsrin 40-cı illәrindә verilmişdir.














