ƏN KİÇİK KVADRATLAR ÜSULU – xәtalar nәzәriyyәsindә tәsadüfi xәtaları saxlayan ölçmәlәrin  nәticәlәrinә  әsasәn mәchul kәmiyyәtlәrin qabaqcadan qiymәtlәndirilmәsi üçün müәyyәn olunmuş metodlardan biri. Ə.k.k.ü. hәmçinin verilәn funksiyanı digәr (daha sadә) funksiyalarla tәqribi tәsvir etmәk üçün istifadә olunur. Ə.k.k.ü K.Qauss (1794–95) vә A.Lejandr (1805–06) tәrәfindәn tәklif edilmişdir. Əvvәllәr bu üsuldan astronomik vә geodezik müşahidәlәrin nәticәlәrinin yenidәn işlәnmәsi üçün istifadә olunurdu. Ə.k.k.ü.-nun ciddi riyazi әsaslandırılması vә tәtbiq sәrhәdlәrinin qurulması A.A.Markov (1898) vә A.N.Kolmoqorov (1946) tәrәfindәn verilmişdir.

Ə.k.k.ü.-nun mahiyyәti ondan ibarәtdir ki, (Qaussa görә) μ fiziki kәmiyyәtinin dәqiq qiymәtinin müşahidәlәrin nәticәlәrinә görә hesablanmış X tәqribi qiymәti ilә әvәz edilmәsindәki “itki” xәtanın kvadratı, yәni (X – μ)2 ilә düz mütәnasibdir. Bu şәrtlәrdә sistematik xәtası olmayan elә X kәmiyyәtinin optimal qiymәti qәbul edilir ki, onun “itkisinin” orta qiymәti minimum olsun. Mәhz bu tәlәb Ə.k.k.ü.-nun әsasını tәşkil edir. Ümumi halda bu üsul әsasında X-in optimal qiymәtinin tapılması kifayәt qәdәr çәtin mәsәlәdir. Ona görә praktikada bu mәsәlә mәhdudlaşdırılır vә X әvәzinә müşahidәlәrin nәticәsindәn asılı, sistematik xәtası olmayan vә bütün xәtti funksiyalar sinfindә orta “itki” qiymәti minimal olan xәtti funksiya götürülür.

Əgәr müşahidәlәrin tәsadüfi xәtaları normal paylanmaya malikdirsә vә qiymәtlәndirilәn μ kәmiyyәti müşahidәlәrin nәticәlәrinin orta qiymәtindәn xәtti asılıdırsa (bu hala Ə.k.k.ü.-nun tәtbiqi zamanı kifayәt qәdәr tez-tez rast gәlinir), onda bu mәsәlәnin hәlli eyni zamanda ümumi mәsәlәnin hәlli olacaq. Bu halda μ kәmiyyәtinin X optimal qiymәti μ orta qiymәti ilә normal paylanmaya malikdir vә uyğun olaraq X tәsadüfi kәmiyyәtinin ehtimallarının paylanma sıxlığı

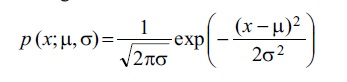
x =X  olduqda,  μ =X  nöqtәsindә  maks.-a  çatır.

Tutaq ki, mәchul μ kәmiyyәti üçün n sayda asılı olmayan müşahidәlәr aparılmışdır: Y₁, Y₂, ..., Y_n, yәni

 Y₁=μ + d₁, Y₂=μ+ d₂, ..., Y_n=μ+ d_n, 

burada d₁,d₂, ..., d_n – tәsadüfi xәtalardır (klassik xәtalar  nәzәriyyәsindәki qәbul edilmiş tәrifә әsasәn tәsadüfi xәtalar riyazi gözlәmәsi sıfır olan asılı olmayan tәsadüfi kәmiyyәtlәrdir, yәni Eδ_i = 0; Eδ_i ≠ 0 olarsa, sistematik xәtalar adlanır). Ə.k.k.ü.-na әsasәn μ kәmiyyәtinin qiymәti kimi elә X qәbul edilir ki,

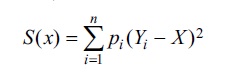
kvadratlar  cәmi  әn  kiçik  olsun  (üsulun adı  buradandır).  Burada   p_i = k/σ_i²    vә σ_i²  = Dδ_i = Eδ²_i (k > 0 әmsalını ixtiyari seçmәk olar). p_i kәmiyyәti çәki, σ_i isә i nömrәli ölçmәnin kvadratik yayınması adlandırılır.

Xüsusi halda ölçmәlәr eynidәqiqlikli olarsa, onda σ₁=σ₂=...= σ_n vә bu halda p₁=p₂=...=p_n=1 fәrz etmәk olar. Əgәr hәr bir Y_i n_i sayda eynidәqiqlikli ölçmәlәrin әdәdi ortasıdırsa, onda fәrz edilir ki, p_i = n_i.  Əgәr X kimi çәkinin orta qiymәtini götürsәk, onda S(X) cәmi әn kiçik olacaq

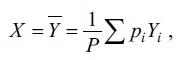
burada P =Σp_i . μ kәmiyyәtinin sistematik xәtası olmayan Y¯ qiymәti P çәkisinә vә DY‾ = k/P dispersiyasına malikdir. Xüsusi halda bütün ölçmәlәr eynidәqiqlikli olarsa, onda ölçmәlәrin nәticәlәrinin әdәdi ortası ( Y^–):

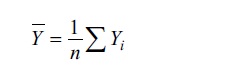
vә DY¯   ≡  σ²/n. Bәzi ümumi hallarda göstәrmәk olar ki, әgәr müşahidәlәrin sayı n kifayәt qәdәr böyük olarsa, onda  qiymәtinin paylanması, μ riyazi gözlәmәsi vә dispersiyası k/P olan normal  paylanmadan  az fәrqlәnir. Bu halda μ ≈ Y¯  tәqribi bәrabәrliyinin mütlәq xәtası inteqralın qiymәtinә yaxın olan ehtimalla t√k/P-dәn azdır:

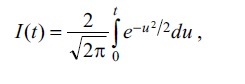
[mәs.,   I (1,96) = 0,950;   I(2,58) = 0,990;  I(3,00) = 0,997].

Əgәr p_i ölçmәlәrinin çәkisi verilәrsә, k vuruğu isә müşahidәlәrә qәdәr mәchul qalarsa, onda bu vuruq vә Y qiymәtinin dispersiyası

 k = S (Y¯)( n –1) vә

DY ¯= k/P ≈ s² = S(Y¯ )/[(n –1)P ]

 (hәr iki qiymәtlәndirmәdә sistematik xәta yoxdur) düsturları ilә tәqribi qiymәtlәndirilә bilәr.

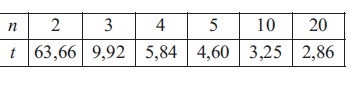
δ _i xәtaları normal paylanmaya tabe olan praktik әhәmiyyәtli halda μ ≈  Y^- tәqribi bәrabәrliyinin mütlәq xәtasının ts-dәn az olması ehtimalının qiymәtini dәqiq tapmaq olar (t ixtiyari müsbәt әdәddir). Bu ehtimal, t-dәn asılı funksiya kimi (n–1) sәrbәstlik dәrәcәsinә malik Styudent paylanma funksiyası adlandırılır vә aşağıdakı düsturla hesablanır:

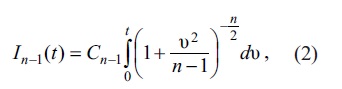
burada C_n–1 sabiti elә seçilib ki, I_n–1(∞)=1 şәrti ödәnsin. n-in böyük qiymәtlәrindә (2) düsturunu (1) düsturu ilә әvәz etmәk olar. Lakin n-in kiçik qiymәtlәrindә (1) düsturunun  tәtbiqi ciddi xәtalara (kobud sәhvlәrә) gәtirәrdi. Mәs., (1) düsturuna әsasәn I = 0,99 qiymәtinә t = 2,58 uyğun gәlir; Kiçik n-lәrdә I_n–1(t) = 0,99 tәnliklәrinin hәlli kimi tәyin olunan t-nin  uyğun hәqiqi qiymәtlәri cәdvәldә veril- mişdir: