ƏVƏZLƏMƏ, v e r i l m i ş ç o x l u ğ u n e l e m e n t l ә r i n i n – çoxluğun hәr bir elementinin (a) hәmin çoxluqdan olan başqa bir elementlә [φ(a)] әvәz edilmәsi; bu halda hәr biri yalnız bir dәfә olmaqla verilmiş çoxluğun bütün elementlәri alınmalıdır. Belәliklә, Ə. anlayışı mahiyyәtcә çoxluğun öz-özünә qarşılıqlı birqiymәtli inikası anlayışı ilә üst-üstә düşür. “Ə.” termini (bәzәn “yer dәyişmә” dә deyirlәr) әsasәn sonlu çoxluqlara tәtbiq olunur. Aşağıda yalnız bu hal nәzәrdәn keçirilәcәk. Ə. anlayışını iki sәtirli simvolla işarә etmәk qәbul olunmuşdur:
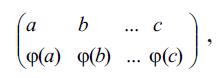
burada verilmiş çoxluğun hәr bir elementinin altında ona uyğun olan element yazılmış dır. Ə.-nin xassәlәri a, b,…, c elementlәrinin tәbiәtindәn asılı olmadığından, çox vaxt 1, 2,…, n tam әdәdlәrindәn istifadә olunur, bu zaman onlar ilk sәtirdә, әsasәn, öz ardıcıl sırası ilә yazılır. Ə.
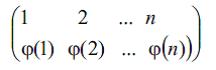
vә ya daha sadә:
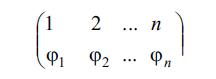
şәklini alır, burada ikinci sәtir φ1, φ2,…, φn – 1, 2, …, n әdәdlәrindәn alınan hәr hansı Ə.-ni әmәlә gәtirir. n elementdәn ibarәt çoxluğun müxtәlif Ə.-lәrinin sayı onun yerdәyişmәlәrinin sayı qәdәrdir, yәni n!=1·2·3·…·n. Bütün elementlәri yerindә saxlayan (dәyişmәyәn) Ə.-yә v a h i d Ə. vә ya e y n i l i k Ə.-si deyilir:

Hәr bir A Ə.-si üçün onun tәrsi olan (yәni φi-ni i-yә çevirәn) Ə. mövcuddur vә A–1 ilә işarә edilir:
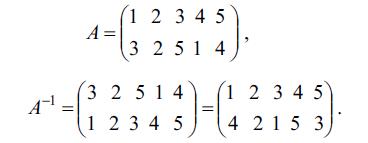
İki ardıcıl A vә B Ə.-lәrinin tәtbiqinin nәticәsi yenidәn hәr hansı C Ə.-si olacaq: әgәr A i-ni φi-yә, B isә φi-ni ψi-yә çevirәn Ə.-dirsә, onda C Ə.-si i-ni ψi-yә çevirir. C Ə.-si A vә B Ə.-lәrinin hasili adlanır, C=AB kimi yazılır. Mәs., әgәr
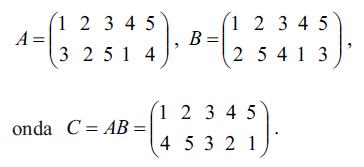
Ə.-lәrin hasili üçün kommutativlik qanunu ödәnmir, yәni ümumiyyәtlә AB≠BA; mәs., hәmin misalda

Asanlıqla görmәk olar ki, IA=AI=A, AA–1=A–1A= I, A(BC)=(AB)C (assosiativlik qanunu). Belәliklә, n elementdәn ibarәt Ə.-lәrin hamısı s i m m e t r i k q r u p adlanan n dәrәcәli qrup әmәlә gәtirir. Yalnız iki i vә j elementlәrinin yerdәyişmәsi ilә tәsvir olunan Ə.-lәr t r a n s p o z i s i y a adlanır vә (i, j) ilә işarә edilir, mәs.,
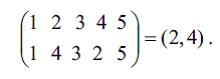
İstәnilәn Ə.-ni transpozisiyaların hasili şәklindә ayırmaq olar. Verilmiş Ə.-nin trans pozisiyaların müxtәlif üsullarla hasili şәklindә ayrılışında vuruqların sayı müxtәlif ola bilәr, lakin onlar hәmişә ya cüt, ya da tәk sayda olacaq. Bununla әlaqәdar Ə. tәk Ə., ya da cüt Ə. adlanır: A = (1,3)(5,4)(5,1) – tәk Ə.-dir. Ə.-nin cütlüyünü yuxarı sәtirdәki әdәdlәr öz ardıcıl sırası ilә verildikdә i n v e r s i y a l a r ı n, yәni aşağı sәtirdәki ardıcıllığın pozulması sayı ilә dә müәyyәn etmәk olar: Ə.-nin cütlüyü inversiyaların sayının cütlüyü ilә üst-üstә düşür; mәs., A Ə.-sinin aşağı sәtrindә 5 inversiya var, yәni böyük әdәd kiçik әdәddәn әvvәl gәlib: (3, 2), (3,1), (2,1), (5,1) vә (5,4). n elementin n!/2 sayda cüt vә n!/2 sayda tәk Ə.-si mövcuddur. Verilmiş elementlәr qrupunu dövri dәyişәn, lakin qalan elementlәri olduğu kimi saxlayan Ə.-yә d ö v r deyilir. Dәyişәn әdәdlәrin sayı d ö v r ü n u z u n l u ğ u adlanır. Mәs., A Ə.-si uz. 4 olan dövrdür: O, 1-i 3-ә, 3-ü 5-ә, 5-i 4-ә, 4-ü 1-ә çevirir, bu, qısa olaraq A(1, 3, 5, 4) kimi yazılır. Transpozisiya uz. 2 olan dövrdür. İstәnilәn Ə.-ni asılı olmayan (yәni ümumi elementlәri olma yan) dövrlәrin hasili şәklindә ayırmaq olar, mәs.,
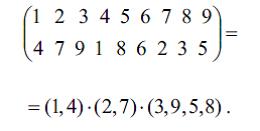
Riyazi analizdә “Ə.” termini dәyişәnin әvәz olunması kimi başa düşülür.














