ƏYRİLİK – әyrinin (sәthin) düz xәtdәn (müstәvidәn) yayınmasını (meylini) xarakterizә edәn kәmiyyәt. L әyrisinin MM′ qövsünün M nöqtәsindә MT toxunanından (şәkil) yayınmasını bu qövsün mәrkәzi Ə.-i adlanan k_m ilә xarakterizә etmәk olar. Bu kәmiyyәt M vә M′ nöqtәlәrindәn çәkilәn toxunanalar arasındakı α bucağının MM′ qövsünün Δs uz.-na olan nisbәtinә bәrabәrdir (α ⁄Δs). Çevrәnin qövsünün mәrkәzi Ə.-i radiusun tәrs qiymәtinә bәrabәrdir vә çevrәnin Ə. dәrәcәsini xarakterizә edir. Radiusun azalması ilә qövsün Ə.-i artır.

Δs→0 olduqda, yәni M nöqtәsi M′-ә yaxınlaşdıqda, mәrkәzi Ə.-in limit qiymәti L әyrisinin M nöqtәsindәki k Ə.-i adlanır:

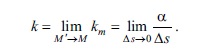
Ə.-in tәrs qiymәti R = 1/k L әyrisinin M nöqtәsindәki Ə. radiusuna deyilir.

Əgәr L y =f (x) funksiyasının qrafikidirsә, onda bu әyrinin x nöqtәsindәki k Ə.-i

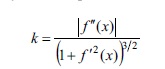
 düsturu ilә hesablanır. L әyrisinin k Ə.-i bu әyrinin hәr hansı M nöqtәsindәn hesablanan s qövsünün uz. funksiyasıdır.

Sәthin M nöqtәsindәki normalından keçәn bütün mümkün müstәvilәrin sәthlә kәsişmәsinә normal kәsiklәr, M nöqtәsindәn keçәn normal kәsiklәrin Ə.-ni isә sәthin bu nöqtәsindәki normal Ə.-lәri adlandırırlar. M nöqtәsindә verilmiş normal Ə.-in maks.-u vә minimumuna baş Ə.-lәr deyilir. K = k₁k₂ vә H= (k₁+k₂)/2 kәmiyyәtlәri M nöqtәsindә uyğun olaraq sәthin Qaus Ə.-i vә mәrkәzi Ə.-i adlanır, burada k₁ vә k₂ – baş Ə.-lәrdir. Sәthin bu Ə.-lәri normal Ə.-i tәyin edir, ona görә dә onlar sәthin müstәvidәn yayınmasını xarakterizә etmәyә yardımçı ola bilәr. Adәtәn sәthin bütün nöqtәlәrindә K = 0 vә H = 0-dırsa, onda o müstәvidir.

Ə. anlayışı daha ümumi tәbiәtli obyektlәrә ümumilәşdirilir. Mәs., o, Riman fәzalarında, hәmin fәzaların Evklid fәzalarından yayınma ölçüsünü tәsvir edәrkәn yaranır.