FREDHOLM ALTERNATİVİ – ikinci növ Fredholm tәnliyinin

hәlli varlığının tәsdiqi. Daha dәqiq, f vә g-nin necә olmasından asılı olmayaraq, ya (1) vә ona qoşma olan

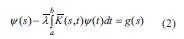
tәnliklәrinin yeganә φ, ψ hәllәri var, yaxud uyğun bircins ( f ≡ g ≡ 0 olduqda) tәnliklәrin sıfır olmayan hәllәri var vә hәm dә xәtti asılı olmayan hәllәrin sayı hәr iki tәnlik üçün sonlu vә eynidir. İkinci halda (1) tәnliyinin hәlli olması üçün

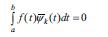
(k =1, ..., n) olması zәruri vә kafidir, burada ψ₁, ..., ψ_n – (2) tәnliyinә uyğun bircins tәnliyin xәtti asılı olmayan hәllәrinin tam sistemidir. Bu halda (1) tәnliyinin ümumi hәlli

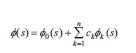
şәklindәdir, burada φ₀ – (1) tәnliyinin hәlli, φ₁, ... , φ_n (1) tәnliyinә uyğun bircins tәnliyin xәtti asılı olmayan hәllәrinin tam sistemidir, c₁, ..., c_n – ixtiyari sabitlәrdir. Oxşar tәsdiq (2) tәnliyi üçün dә ödәnir. F.a., E.İ.Fredholm tәrәfindәn isbat olunmuşdur (1903).