FURYE İNTEQRALI – qeyri-periodik funksiyanın harmonik komponentlәrә ayrılışı üçün düstur. Əgәr f(x) funksiyası hәr bir sonlu parçada mütlәq inteqrallanandırsa vә yığılırsa, yәni

Bu düstura ilk dәfә J.Furyenin bәzi istilikkeçirmә mәsәlәlәrinin hәllindә rast gәlinir (1811), lakin onun isbatı sonradan başqa riyaziyyatçılar tәrәfindәn verilmişdir. (1) düsturunu hәmçinin

(2) düsturuna 2T periodlu funksiyanın Furye sırasının limit forması kimi baxmaq olar (T→∞ olduqda). Bu halda a(u) vә b(u) f(x) funksiyasının Furye әmsallarına analojidir. Kompleks әdәdlәri tәtbiq edәrәk (1) düsturunu

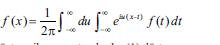
düsturu ilә әvәz etmәk olar.(1) düsturunu hәmçinin

kimi dә çevirmәk olar (s a d ә   F u r y e   i n t e q r a l ı). 

Əgәr (2), (3) düsturlarındakı inteqrallar dağılırsa, onda bir çox hallarda onları bu vә ya başqa şәkildә cәmlәmә üsulu ilә f(x) funksiyasına cәmlәmәk olar. Bir çox mәsәlәlәrin hәllindә iki vә daha çox dәyişәnli funksiyalar üçün Furye inteqralları düsturlarından istifadә olunur.