FURYE METODU – riyazi fizika tәnliklәrini dәyişәnlәrinә ayırmağa әsaslanan hәll metodu. Diferensial tәnliyin başlanğıc bircins vә sәrhәd şәrtlәrini ödәyәn hәllini F.m. ilә tapmaq üçün onun sәrhәd şәrtlәrini ödәyәn xüsusi hәllәri fәza dәyişәnlәrinin funksiyası ilә zamanın funksiyasının hasili şәklindә axtarılır. Xüsusi halda, funksiyanın Furye sırasına ayrılışı vә Furye inteqralı şәklindә göstәrilişi F.m.-nun simin rәqsi vә çubuğun istilikkeçirmә mәsәlәlәrinin hәllinә tәtbiqi ilә bağlıdır. Mәs., ucları bәrkidilmiş l uz.-lu simin kiçik rәqslәrinin öyrәnilmәsi u(0, t)= u(l, t) = 0 sәrhәd şәrtlәrini vә u(x, 0) = f(x), u_t (x, 0) = F(x) (0 ≤ x ≤1) başlanğıc şәrtlәrini ödәyәn 

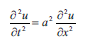
tәnliyinә gәtirilir. Bu tәnliyin X(x)T(t) şәklindә olan vә sәrhәd şәrtlәrini ödәyәn hәlli 

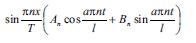
düsturu ilә ifadә olunur. A_n vә B_n-nin әmsallarını uyğun üsulla seçmәklә göstәrmәk olar ki,

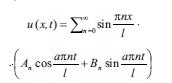
qoyulmuş mәsәlәnin hәllidir.

Bu metodu J.Dalamber dalğa tәnliyinin hәlli üçün tәklif etmişdir (1749), 19 әsrin әvvәllәrindә J.Furye onu kifayәt qәdәr tam şәkildә vermiş, M.V.Ostroqradski isә ümumilәşdirmişdir (1828).