FURYE SIRASI – periodik funksiyanı harmonik komponentlәrә ayırmaq üçün triqonometrik sıra. Əgәr f(x) funksiyası 2T perioduna malikdirsә, onda onun F.s.
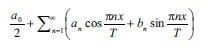
şәklindә olar, burada a0, an, bn (n ≥ 1) – Furye әmsallarıdır. Əmsallar üçün düsturlardakı inteqralların necә anlaşılmasından asılı olaraq, Furye–Riman, Furye – Lebeq vә s. sıralardan danışılır. Adәtәn, 2π periodlu funksiyalara baxılır (ümumi hal buna, asılı olmayan dәyişәnin çevrilmәsi ilә gәtirilir).
F.s. ortoqonal funksiyalar sistemi üzrә әn sadә ayrılışı, daha dәqiq 1, cosx, sinx, cos2x, sin2x, ..., cosnx, sinnx,..., triqonometrik sistemi üzrә ayrılışı özündә ifadә edir ki, o da iki mühüm xassәni – qapalılıq
![]()
şәklindәki xüsusi cәmlәri (Furye cәmlәri)
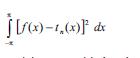
inteqralını minimuma gәtirir, burada tn(x) – dәrәcәsi ≤ n olan istәnilәn triqonometrik polinomdur, f(x) isә kvadratı ilә inteqrallanan funksiyadır. Bu halda
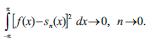
Belә ki, kvadratı inteqrallanan f(x) funksiyası orta kvadratik yayınma mәnasında öz Furye cәmlәri ilә istәnilәn dәrәcәdә yaxşı approksimasiya edir.
İstәnilәn inteqrallanan f(x) funksiyasının an, bn Furye әmsalları n→ ∞ olduqda sıfra yaxınlaşır (B.Riman, A.Lebeq). Əgәr f(x) funksiyası Rimana görә qeyri-mәxsusi inteqrallanırsa, onda Furye әmsalları sıfra yaxınlaşmaya da bilәr (Riman).
Əgәr f (x) funksiyasının kvadratı inteqrallanırsa, onda,
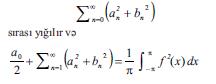
P a r s e v a l b ә r a b ә r l i y i ödәnir. Bu düsturun variantlarından biri fransız riyaziyyatçısı M.Parseval tәrәfindәn göstәrilmişdir (1799), ümümi düsturu isә Lebeq (burada inteqral Lebeq inteqralı mәnasında başa düşülür) isbat etmişdir. Tәrsinә, istәnilәn an, bn hәqiqi әdәdlәr ardıcıllığının
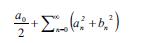
yığılan sırası üçün Furye әmsalları bu әdәdlәr olan, Lebeqә görә kvadratı ilә inteqrallanan funksiya mövcuddur, (alman riyaziyyatçısı E.Fişer, macar riyaziyyatçısı F. Riss) Riman аnlamında inteqrallar üçün bu teorem doğru deyil.
F.s.-nın yığılması üçün çoxlu әlamәtlәr, yәni sıranın yığılmasına zәmanәt verәn kafi şәrtlәr mәlumdur. Birinci yığılma әlamәtini P.Dirixle vermişdir (1829). Mәs., әgәr f(x) funksiyasının dövründә sonlu sayda maks.-lar vә minimumlar mövcuddursa, onda onun F.s. hәr bir nöqtәdә yığılır (P.Dirixle). Daha ümumi, әgәr f(x) mәhdud dәyişmәyә malikdirsә, onda onun F.s. hәr bir nöqtәdә yığılır, f(x)-in kәsilmәz olduğu parçaların daxilindәki parçaların hәr birindә isә müntәzәm yığılır (K.Jordan). Əgәr f(x) kәsilmәzdirsә vә onun ω kәsilmәzlik modulu
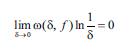
şәrtini ödәyirsә, onda onun F.s. müntәzәm yığılır (italyan riyaziyyatçısı Dini, 1880).
Riman göstәrmişdir ki, F.s.-nın hәr hansı x0 nöqtәsindә yığılması vә ya dağılması, f(x) funksiyasının hәmin nöqtәnin istәnilәn qәdәr kiçik әtrafında özünü necә aparmasından asılıdır (F.s. üçün l o k a l i z a s i y a p r i n s i p i). Əgәr f(x) funksiyası x0 nöqtәsindә birinci növ kәsilmәyә malikdirsә, yәni, müxtәlif f(x0 – 0) vә f(x0 + 0) limitlәri mövcuddursa vә bu funksiyanın F.s. x0 nöqtәsindә yığılırsa, onda o, 1/2{f(x0 – 0) + f(x0 + 0)} qiymәtinә yığılır. Xüsusi halda, kәsilmәz dövri f(x) funksiyasının F.s. hәr bir nöqtәdә yığılırsa, onda onun cәmi f(x)-ә bәrabәrdir.
Mәlumdur ki, F.s. sonsuz sayda nöqtәlәrdә dağılan (alman riyaziyyatçısı P. dyu Bua-Reymon, 1875) vә F.s. hәr bir nöqtәdә dağılan Lebeq аnlamında inteqrallanan funksiyalar mövcuddur (A.N.Kolmoqorov, 1926). Lakin kvadratı ilә inteqrallanan funksiyaların F.s. sanki hәr yerdә yığılır. (L.Karleson, 1966). Bu nәticә p < 1 olduqda istәnilәn Lp(–π, π) fәzasından olan funksiyalar üçün dә doğrudur (R. Hant, 1968). Adları çәkilәn “yığılma defektlәri” F.s.-nın c ә m l ә m ә m e t o d u n u әmәlә gәtirmişdir. Furye cәmlәrinin özünü aparmasını araşdırmaq әvәzinә, bu cәmlәrdәn yaradılmış orta qiymәtә baxılır ki, bu da digәr hallardan daha dәqiq olur. Mәs., istәnilәn kәsilmәz periodik f(x) funksiyasının
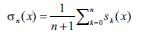
F e y e r c ә m i n→∞ olduqda f(x) funksiyasına müntәzәm yığılır (L. Feyer, 1904).














