GİBBS PAYLANMALARI – çoxlu sayda zәrrәciklәrdәn ibarәt olan sistemin müxtәlif fiziki şәraitlәrdә reallaşa bilәn hallarda olma ehtimallarının tarazlı paylanmaları. Statistik fizikanın fundamental qa- nunlarından olan G.p. 1901 ildә C.U. Gibbs tәrәfindәn kәşf edilmiş vә 1927 ildә C. fon Neyman tәrәfindәn ümumilәşdirilәrәk kvant statistik mexanikaya tәtbiq edilmişdir.

G.p.-nı almaq üçün Gibbsin statistik ansamblı anlayışından istifadә edilir. Verilmiş makroskopik şәrtlәr daxilindә, N sayda zәrrәciklәrin q = (q₁, q₂, …, q_N) koordinatları vә р = (р₁, р₂, …, p_N) impulsları ilә xarakterizә olunan müxtәlif mikrohallara uyğun gәlәn, müәyyәn fiksә olunmuş makroskopik sistemin böyük (limitdә sonsuz böyük) sayda kopiyaları çoxluğuna Gibbsin statistik ansamblı deyilir. Yәni, (p, q) faza fәzasında mümkün olan sistemlәrin (ansamblın elementlәrinin) paylanmasına baxılır. Klassik statistikada G.p. zamandan asılı deyil; koordinat vә impulslardan asılılıqlar isә yalnız Hamilton funksiyası H(p, q) vasitәsilә baş verir.

Sabit V hәcmindә yerlәşәn, E enerjisinә malik N sayda zәrrәciklәrdәn ibarәt vә әtraf mühitdәn energetik izolә olunmuş (Gibbsin mikrokanonik ansamblı) sistemlәr çoxluğu G i b b s i n   m i k r o k a n o n i k   p a y l a n m a  f u n k s i y a s ı  f(p, q) ilә ifadә olunur vә bu sistemin bütün halları E enerjisi әtrafında dar bir zolaqda (ΔE<< E) eyniehtimallıdır (statistik mexanikanın әsas hipotezi).

Termostatla kontaktda olan, yәni termostatın mütlәq T temp-runda verilmiş V hәcmini tutan, N sayda zәrrәciklәrdәn ibarәt olan vә dәyişәn enerjiyә (ancaq enerjinin orta qiymәti sabitdir) malik olan (Gibbsin kanonik ansamblı) sistemlәr çoxluğu G i b  b s i n   k a n o n i k   p a y l a n m a  f u n k s i y a s ı  ilә ifadә olunur:

burada T – mütlәq temp-r, F – sәrbәst enerji (Helmholts enerjisi), k – Boltsman sabitidir.

Termostatla vә zәrrәciklәr rezervuarı ilә kontaktda olan, yәni dәyişәn sayda N zәrәciklәrdәn ibarәt olan vә verilmiş T temp-r vә μ kimyavi potensial üçün H_N Hamilton funksiyası ilә tәyin olunan enerjiyә malik olan (Gibbsin böyük kanonik ansamblı) sistemlәr çoxluğu G i b b s i n  b ö y ü k  k a n o n i k   p a y l a n m a   f u n k s i y a s ı  ilә ifadә olunur:

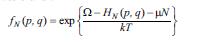
burada Ω – ehtimalın normallaşma şәrtindәn tәyin olunan vә V, μ, T dәyişәnlәrindәn asılı olan termodinamik potensialdır.

Ətraf mühitlә termik vә mexaniki kontaktda olan, yәni sabit tәzyiqdә (mәs. hәrәkәt edә bilәn porşenin hesabına) dәyişәn enerji vә hәcmә malik olan (Gibbsin izobar-izotermik ansamblı) sistemlәr çoxluğu G i b b s i n   i z o b a r - i z o t e r m i k   p a y l a n m a  funksiyası ilә ifadә olunur:

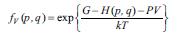
burada G – Gibbs enerjisi, yәni V, P, T dәyişәnlәri ilә ifadә olunan termodinamik potensialdır.

Klassik statistik mexanikadakı G.p. kvant statistik mexanikadakı G.p.-nın xüsusi halıdır; zәrrәciklәrin sıxlığının vә temp-runun elә qiymәtlәri mövcuddur ki, bu halda kvant effektlәrinin tәsirini nәzәrә almamaq olur.

Bütün G.p. müxtәlif әlavә şәrtlәr daxilindә informasion entropiyanın (bax Entropiya) maksimumuna uyğun gәlir; belә ki, mikrokanonik G.p.-nda bu zәrrәciklәrin sayının vә enerjinin sabit olduğu hala; kanonik G.p. – zәrrәciklәrin sayının sabit vә orta enerjinin isә verilmiş olduğu hala; böyük kanonik G.p. – orta enerjinin vә zәrrәciklәrin orta sayının verilmiş qiymәtlәri daxilindә malik olduğu hala uyğun gәlir. Demәli, bütün G.p. müxtәlif şәrtlәr daxilindә әn ehtimallı paylanmanı әks etdirir.