БОГОЛЙÚБОВУН ТЯНЛИКЛЯР СИЛСИЛЯСИ -  Н зярряъиклярдян ибарят классик статистик системдя с зярряъиклярин координат вя импулсларынын F_с(т,р₁,…,р_с, п₁,…,п_с) пайланма функсийалары цчцн тянликляр силсиляси, бурада с=1,2,…, Н–1, т – заман, р₁,…,р_с вя п₁, …, п_с – зярряъиклярин координат вя импулсларынын цчюлчцлц векторларыдыр. Пайланма функсийаларынын (ясасян, Ф₁ вя Ф₂₎ кюмяйи иля статистик системлярин бцтцн спесифик характеристикалары ифадя олуна биляр. Ф_с пайланма функсийалары (даща дя- гиг, пайланма сыхлыьы) ашаьыдакы бярабярликлярля тяйин олунур: F_с(т, р₁,…,р_с, п₁,…, п_с) = V ^с∫ω_Nдр_{с+ 1}… др_Ндп_с+1…дп_Н; бурада с = 1, 2,…, Н–1, В– системин щяъми, ω_Н – Лиувилл тянлийини юдяйян _Н зярряъикляр цчцн пайланма функсийасыдыр (ещтималларын пайланма сыхлыьы), бурада Щ_Н – Н зярряъикляр системинин щамилтонианыдыр; фигурлу мютяризяляр Пуассон мютяризялярини ифадя едир (ашаьы бах). ω_Н-дян фяргли олараг Ф_с функсийалары нормалаш- дырылмайыб вя В^_с кямиййяти иля нормалашдырылдыгда ещтималларын пайланма функсийалары олур.
      Лимит щалында В → ∞, В/Н = υ (υ – мцсбят сабитдир) олдугда Б.т.с. юзцнц с-нъи тянлийи Ф_с+1 функсийасы иля ∂Ф_с/∂т тюрямясини ялагяляндирян сонсуз тянликляр системи кими эюстярир:

                                                                                                                                                                                       
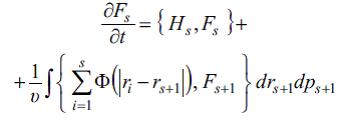
    Бурада Ф(|р_и – р_с+1|) – и-нъи вя (с+1)- инъи зярряъиклярин гаршылыглы тясир потенсиалы, Щ_с – с зярряъикляр системинин щамилтонианыдыр (кинетик вя потенсиал енержилярин ъями); фигурлу мютяризяляр Пуассон мютяризяляри олуб, р₁,…,р_с, п₁,…,п_с Щамилтон (каноник) дяйишянляринин ф(т,р₁,…, р_с, п₁,…, п_с) вя э(т,р₁,…,р_с, п₁,…, п_с) функсийалары цчцн ашаьыдакы бярабярликля тяйин олунур: 
                                                                                                                          
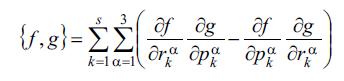
      Бурада   вя  , α = 1, 2, 3 – зярряkъиклярин координат вя импулсларынын компонентляридир, к=1,…, с. 
      Б.т.с.-нин тядгигинин ясас чятинликляри системин гапалы олмасы вя бу системин щяллинин Ф_с функсийасына гойулан хцсуси сярщяд шяртляри иля тапылмасы проблемляри иля баьлыдыр. Щяр бир зярряъийин импулслара эюря пайланмасы Максвелл пайланмасы олан термодинамик таразлыг щалында вя щямчинин гыса вя узунтясир щалларында (уйьун олараг зярряъиклярин гаршылыглы тясиринин еффектив радиусунун цчцнъц дяряъяси υ параметриня нисбятян аз олан вя υ-ни хейли ютцб кечян щаллар) бу тядгигатлар бир гядяр садяляшир. Б.т.с. хцсуси щалда Ф₁ бирзярряъикли пайланма функсийасы цчцн Болтсманын кинетик тянлийиня эятирир. 
     Квант статистик системляря бахылдыг- да Б.т.с. с – натамам статистик квант операторларына эюря гурулур. 
   Ф_с пайланма функсийалары цчцн тянликляр силсилясиндян истифадя етмякля статистик системлярин юйрянилмясиня аид олан йанашма 1946 илдя Н.Н. Боголйубов тяряфиндян тяклиф олунмуш вя беля тянликляр силсиляси Б.т.с. адландырылмышдыр. Ону щямчинин ББГКИ тянликляри дя адландырырлар, бу ад Б.т.с.-нин тядгигиндя чох мцщцм рол ойнайан Н.Н. Боголйубовун, М. Борнун, инэилис алимляри Ъ. Гринин, Ъ. Кирквудун вя Ъ. Айвонун адлары иля баьлыдыр.
     Б.т.с. статистик механикада классик вя квант системлярин юйрянилмяси цчцн ясас апаратдыр.