BÓLТSMAN ПАЙЛАНМАСЫ – хариъи потенсиал сащядя йерляшян вя классик механикайа табе олан идеал газ зярряъикляринин (атомларын, молекулларын) импулслара (п) вя координатлара (р) эюря статистик таразлыг пайланма функсийасы ф( п, р): 

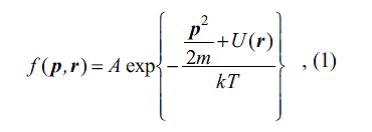
бурада – м кцтляли зярряъийин кинетик енержиси, У(р) – хариъи сащядя онун потенсиал енержиси, Т – газын мцтляг темп-ру, к – Bolтsman сабитидир. А сабити ф ( п, р)-дян бцтцн п вя р-ляря эюря алынан интегралын системдя олан Н зярряъиклярин там сайына бярабярлийи шяртиндян (нормалашдырма шярти) тяйин олунур. Хцсуси щалда У(р)=0 олдугда Б.п. сцрятляря эюря Максвелл пайланмасына кечир. Зярряъикляри арасында гаршылыглы тясир нязяря алынмайан газ цчцн Б.п. Эиббс пайланмасындан алына биляр. Зярряъикляр бир-бири иля гаршылыглы тясирдя олмадыьындан, системин щамилтонианыны айры-айры зярряъиклярин щамилтонианларынын ъями шяклиндя тясвир етмяк вя пайланмайа Эиббсин статистик механикасындакы кими бцтцн зярряъиклярин фаза фязасында йох, бир zяrrяciйин координат вя импулсларынын фаза фязасында бахмаг олар. (1) пайланма функсийасыны бязян Максвелл–Bolтsman пайланмасы, Bolтs- man пайланмасыны ися зярряъиклярин бцтцн импулсларына эюря интегралланмыш (1) пайланма функсийасы адландырырлар (о, р нюгтясиндя зярряъикляр сайынын н сыхлыьыны характеризя едир):

н(р)=н0ехп{– У(р)/кТ},

бурада н0 – У(р)=0 олан нюгтяйя уйьун зярряъикляр сайынын сыхлыьыдыр. Мцхтялиф нюгтялярдя (р1 вя р2) зярряъикляр сайынын сыхлыглары (н1 вя н2) нисбяти бу нюгтялярдя зярряъиклярин потенсиал енержиляри фяргиндян асылыдыр: 

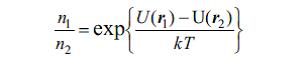
Хцсуси щалда бурадан Йерин сятщи цзяриндяки аьырлыг сащясиндя щ щцндцрлцкдян асылы олараг зярряъикляр сайынын пайланма сыхлыьыны тяйин едян барометрик дцстур алыныр. Бу щалда щ)=мэщ, бурада э – аьырлыг гцввяси тяъили, м – зярряъийин кцтлясидир. Идеал квант газлары цчцн айры-айры zяrrяciklяrin щалы импулс вя координатларла йох, У(р) сащясиндя зярряъийин Eи енержисинин квант сявиййяляри иля тяйин едилир. Бу щалда и-ъи квант щалындакы зярряъиклярин ni орта сайы цчцн Б.п. беля шякил алыр:

ni =ехп [(μ – Eи)/кТ ], (2)

бурада μ – кимйяви потенсиалдыр. (2) дцстуру газын квант ъырлашмасы нязяря алынмайан, лакин зярряъиклярин енержи сявиййяляринин квантланмасы нязяря алынан темп-р вя сыхлыгларда Бозе–Ейнштейн пайланмасы вя Ферми–Дирак пайланмасынын щядд щалыдыр.