там нормалашмыш хятти фяза. Б.ф. мцасир рийази vя функсионал анализин ян мцщцм анлайышларындан биридир; Б.ф.-нын цмуми тярифини вермиш вя беля фязаларын ардыъыл юйрянилмясиня башламыш С. Банаxын ады иля баьлыдыр. 20 ясрин яввялляриндя Д. Щилберт, А. Лебег, М. Фреше, Ф. Рисс тяряфиндян дахил едилмиш функсийалар фязасы вя ардыъыллыглар фязасы Банаxын арашдырмалары цчцн база олмушдур.
Б.ф.-нда хятти гурулушун олмасы эюстярир ки, бу фязада елементлярин комплекс (вя йа щягиги) ядядляря вурулмасы вя ихтийари елемент ъцтляри цчцн онларын ъями тяйин едилмишдир. Топлама вя вурма ямялиййатлары вектор фязасынын аксиомларына табедир. Хятти фяза о вахт нормалашмыш адланыр ки, онун щяр бир х елементиня уйьун олараг мянфи олмайан еля ||x|| ядяди гаршы гойулсун ки, 1) йалныз вя йалныз x=0 олдугда ||x||=0; 2) щяр щансы комплекс (вя йа щягиги) λ ядяди цчцн ||λ x||=|λ| ||x||; 3) хятти фязанын истянилян x вя й ъцтляри цчцн ||x+й|| ≤ ||x|| + ||й|| олсун. ||x|| ядяди x елементинин нормасы адланыр. Нормалашмыш X фязасынын тамлыьы о демякдир ки, к, н→∞ олдугда, ||xк– xн||→0 шяртини юдяйян X-дян олан истянилян хк елементляр ардыъыллыьы цчцн X фязасында еля x елементи вар ки, к→∞ олдугда, ||x– xк||→ 0 олсун. 
Б. ф-нын мцщцм хцсуси щалы кими хятти гурулушла йанашы (x,й) скалйар щасили верилян Щилберт фязасыны эюстярмяк олар; бурада

 

Сепарабел Б.ф. хцсуси рол ойнайыр. Нормалашмыш X фязасы о вахт сеперабел фяза адланыр ки, орада Х-дя сых олан {x1, x2,…} елементляринин щесаби чохлуьу олсун, йяни истянилян ε >0 вя Х-дян олан истянилян x елементи цчцн {x1, x2,…} чохлуьундан еля xк елементи тапылаъаг ки, ||x–xк||< ε олсун. Максимуму х∈[а,б] цзря эютцрцлян

нормалы [а,б] парчасында кясилмяз ф(x) функсийаларынын Ъ [а,б] фязасы, Лебег цзря п-дяряъядян интегралланан функсийалардан ибарят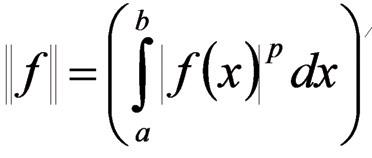  

нормалы Лп[а,б], п≥1 фязасы, x=(x1, x2,…)-дян ибарят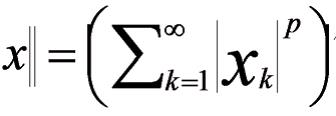



нормалы лп, п≥1 сонсуз ардыъыллыглар фязасы Б.ф.-на мисал ола биляр. Бцтцн бу фязалар сепарабел, Л2[а, б] вя л2 фязалары ися Щилберт фязаларыдыр. Мцасир анализдя мцхтялиф конкрет функсионал Б.ф.-ндан, хцсуси щалда Соболев, Щарди, Бесов фязаларындан истифадя олунур. 
Б Б.ф. иля йанашы она гошма олан Б* фязасына бахылыр. Б* фязасы Б-дя хятти кясилмяз функсионаллардан, йяни комплекс (вя йа щягиги) ядядляр мейданында Б фязасынын хятти кясилмяз иникасларындан ибарятдир. || ф ||=суп | ф(x)| нормалы Б* фязасы да (бурада супремум ||x||≤1 шяртини юдяйян бцтцн x-ляря эюря эютцрцлцр) Б.ф.-дыр. Ашаьыда адлары чякилян теоремляр Б.ф. нязяриййясиндя мцщцм рол ойнайыр: габарыг функсионалларын табелийи сахламагла Б.ф. алтфязасындан бцтцн фязайа давамынын мцмкцнлцйц щаггында Щан–Банах теореми (хцсуси щалда, норманы артырмамаг шяртиля хятти функсионалларын давамынын мцмкцнлцйц); мцнтязям мящдудлуг щаггында Банах–Штейнщауз теореми (бу теоремдя исбат олунур ки, Ан хятти мящдуд операторлар ардыъыллыьы елядир ки, Б.ф.-нын щяр бир х елементи цчцн ||Анх|| ядяди ардыъыллыьы н вя х-дян асылы олмайан щансыса Ъ сабити иля мящдуддур: ||Анх||≤Ъ||х||); тярс оператор щаггында Банах теореми
(бу теоремдя исбат олунур ки, яэяр хятти кясилмяз оператор бир Б.ф.-ны башгасына гаршылыглы биргиймятли иникас етдирирся, онда тярс оператор да кясилмяздир).