BЮYЦK ЯDЯDLЯR QANUNU – son dяrяcя цmumi шяrtlяr дахилиндя, demяk olar ki, tяsadцfdяn asыlы olmayan nяticяyя gяtirян bюyцk sayda tяsadцfi amillяrin birgя яmяlinя уйьун олан цmumi prinsip. Сынагларын sayыnыn artmasы ilя ehtimalлы tяsadцfi hadisяnin baшвермя tezliyinin yaxыnlaшmasы (tezliklяrin dayanыqlыьы adlanan) bu prinsipin iшinя misal ola bilяr.
17–18 яsrлярдя Y. Bernulli асылы олмайан сынаглар ардыъыллыьындакы сынагларын щяр бириндя щяр щансы A hadisяsinin baшвермя ehtimalыnыn eyni bir p, 0<p<1 qiymяtinя malik olmasыnы tяsdiq edяn teoremi isbat етмишдир. Истянилян qeyd olunmuш ε>0 vя n → ∞ цчцн
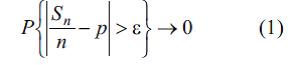
мцнасибяти doьrudur, burada Сн – ilk n сынагда A hadisяsinin baшvermяlяrinin sayы, Сн ⁄н – baшvermяlяrin tezliyi, P – mюtяrizяlяrdя gюstяrilяn hadisяnin ehtimalыдыр. S. Puasson Bernulli teoremini асылы олмайан сынаглар ardыcыllыьыnda A hadisяsinin baшvermя ещтималынын сынаьын nюmrяsindяn asыlы ola bilяъяйи hal цчцn geniшlяndirmiшdir. Тутаг ki, k-ncы сынаг цчцn bu ehtimal pк-ya bяrabяrdir, k=1, 2,..., vя тутаг ki,
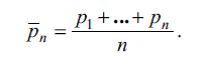
Onda Puasson шяклиндяки B.я.q. n →∞ олдугda истянилян qeyd olunmuш ε >0 цчцn
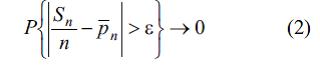
олдуьуну щюкм едир. Bu щюкмцн ъидди исbatыnы P.L. Чebышev vermiшdir (1846). “Bюyцk яdяdlяr qanunu” terminiня ilk dяfя Puаssonda rast gяlinir, o, yuxarыda gюstяrilяn Bernulli teoreminin цmumilяшdirilmяsini belя adlandыrmышdыr. Tяsadцfi Сн kяmiyyяtlяrini Сн=Х1+…+Хн асылы олмайан tяsadцfi kяmiyyяtlяrin cяmi шяklindя ифадя етмяк mцmkцn olarsa, Bernulli vя Puassonun щюкмlяrinin sonrakы цmumilяшdirmяlяri meydana чыxыr, burada A k-нcы сынагда baш verяrsя, Хк=1, яks halda, Хк=0, k=1,...,n. Bu zaman E(Сн ⁄н) riyazi gюzlяmяsi Bernulli halы цчцn p-yя, Puasson halы цчцn — пн-я bяrabяrdir. Baшqa sюzlя, hяr iki halda Х1,…,Хн orta hesabi kяmiyyяtlяrinin рийази gюzlяmяlяrinиn orta hesabiдян йайынмасыna baxыlыr.
P.L. Чebышev “Orta kяmiyyяtlяr haqqыnda” olan iшindя (1867) mцяyyяn eтmiшdi ki, qeyd olunmuш hяr hansы ε > 0 vя n → ∞-da даща цmumi фярзиййяляря gюrя асылы олмайан Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn
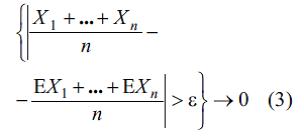
мцнасибяти doьrudur. Чebышev fяrz edиrdi ki, ![]() рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
![]() =DX1+...+DXн= o(n2)
=DX1+...+DXн= o(n2)
шяrtinin юdяnmяsi kifayяtdir. Bеляликля, Чebышev Bernulli teoreminin geniш цmumilяшdirilmяsiнин мцмкцнлцйцнц gюstяrdi. A.A. Markov sonrakы цmumilяшdirmяlяrin мцмкцнлцйцнц гейд етди vя “B.я.q.” adыnыn Bernulli teoreminin цmumilяшdirmяlяrinin bцtцnlцklя hamыsыna, o cцmlяdяn (3)-я tяtbiq olunmasыnы tяklif etdi. Чebышev цsulu riyazi gюzlяmяlяrin цmumi xassяlяrinin мцяййян едилмясиня vя Чebышev bяrabяrsizliyi adlanan bяrabяrsizliyin istifadя olunmasыna яsaslanыr. B.я.q. mцxtяlif formalarыnыn sonrakы isbatlarы Чebышev цsulunun bu vя ya диэяр dяrяcяdя inkiшaf etdirilmяsidir. Markov Хк tяsadцfi kяmiyyяtlяrinin lazыmi “kяsilmяsini” [onlarыn ⎥Xk –EXk⎥≤ tn olarsa, Хн, к=Хк, яks halda sыfra bяrabяr olan (тн yalnыz n-dяn asыlыdыr) Хк, н kюmяkчi kяmiyyяtlяrlя яvяz edilmяsi] tяtbiq edяrяk, B.я.q.-nу toplananlarыn dispersiyalarыnыn olmadыьы hallara da aid etmiшdi. Mяs., o gюstяrmiшdi ki, яgяr hяr hansы δ>0 яdяdi цчцn E⎥Xк – EXк⎥1+δ kяmiyyяtlяri eyni bir sabitlя mяhdudlaшmышsa, (3) ifadяsi юdяnir.
Analoji olaraq Xinчin teoremi (1929) isbat olunur: яgяr Х1, Х2,… eyni paylanma qanuнуna malikdirsя vя EX1 mюvcudдурса, onda (3) B.я.q. доьрудур.
B.я.q.-nun юdяnmяdiyi nцmunяlяr dя var. Mяs., Х1, Х2,… tяsadцfi kяmiyyяtlяri Koшi paylanmasыna, yяni 1/(π(1+х2)) sыxlыqlы paylanmaya malik olarsa, бу ганун юdяnmir. Burada ilk n tяsadцfi kяmiyyяtlяrin (Х1+…+Хн) /н orta hesabisi, ixtiyari n-dя ayrы-ayrы toplananlarда олдуьу kimi, eyni бир paylanmaya malikdir. Koшi paylanmasы цчцn riyazi gюzlяmя mюvcud deyil.
B.я.q.-nun asыlы kяmiyyяtlяrin cяminя tяtbiq edilmяsi ilk nюvbяdя Хи vя Хж tяsadцfi kяmiyyяtlяrinин нюмряляри fяrqinин, yяni ǀи–жǀ-нин artmasы вя onlar arasыndakы asыlыlыьыn azalmasы ilя ялагядардыр. Buna uyьun teoremlяr ilk dяfя A.A. Markov tяrяfindяn Markov zяnciri ilя baьlы olan kяmiyyяtlяr цчцn isbat edilmiшdir (1907).
Сн /н-in Ан= (EX1+...+EXн)/n-dяn йайынмасы haqqыnda tяsяvvцrц Чebышev bяrabяrsizliyi vя onun dяqiqlяшdirmяlяri ilя yanaшы, mяrkяzi лимит teoremi verir.
Deyilяn nяticяlяri mцxtяlif istiqamяtlяr цчцn цmumilяшdirmяk olar. Mяs., yuxarыda hяr yerdя ehtimala gюrя йыьылма адланан yыьыlmaya baxыlыrdы. Baшqa nюv yыьыlmalara, mяs., orta kvadratik vя 1 ehtimallы (санки yяqin yыьыlma) yыьыlmalara da baxыrlar. B.я.q.-nun 1 ehtimallы yыьыlma halы цчцn цmumilяшdirilmяsini gцclяndirilmiш B.я.q. adlandыrыrlar.
Тутаг ki, Х1, Х2,… tяsadцfi kяmiyyяtlяr ardыcыllыьыdыr vя яvvяlki kimi Сн=Х1,+…+Хн. Яgяr Ан sabitlяrinin elя ardыcыllыьы mюvcuddursa ki, Сн /н–Ан→0 ifadяsinin ehtimalы н→∞ олдугда 1-яbяrabяr olsun, onda deyirlяr ki, Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu юdяyir. Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu yalnыz vя yalnыz onda юdяyir ki, ixtiyari qeyd olunmuш ε >0 цчцн
bяrabяrsizliклярinin eyni zamanda юdяnmяsi ehtimalы н→∞-da 1-я yaxыnlaшыr. Belяliklя, burada bцtцn cяmlяr ardыcыllыьыna бцтювлцкдя baxыlыr, adi B.я.q.-nda isя sюhbяt yalnыz ayrы-ayrы cяmlяrdяn gedir. Яgяr Х1,Х2,… ardыcыllыьы gцъlяndirilmiш B.я.q.-nu юdяyirsя, onda o hяmin Ан-lяr цчцн adi B.я.q.-nu da юdяyir, йяни ixtiyari qeyd olunmuш ε > 0-da vя н → ∞-da
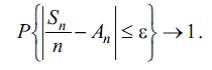
Тярси, цmumiyyяtlя, doьru deyil.
Bernulli sxemi цчцn gцclяndirilmiш B.я.q. ilk dяfя E. Borel tяrяfindяn dяqiq ifadя edilmiш vя isbat olunmuшdur (1909).
Асылы олмайан toплаnanlar цчцn gцclяndirilmiш B.я.q.-nun doьru olmasыnыn A.N. Kolmoqorov tяrяfindяn mцяyyяn edilmiш шяrtlяri daha чox mяшhurdur: sonlu dispersiyalы kяmiyyяtlяr цчцn kafi (1930), eyni cцr paylanmыш kяmiyyяtlяr цчцn щям zяrurи, щям дя kafi (bu kяmiyyяtlяrin riyazi gюzlяmяsinin варлыьы ilя нятиъяляняn). Асылы олмайан sonlu dispersiyalы Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn Kolmoqorov teoremi щюкм едир ки, Aн=E(Сн /н) olmaqla
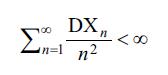
шяrtindяn gцclяndirilmiш B.я.q.-нун doьruлуьу алыныр.

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, “Azərbaycan” xüsusi cildi (Azərbaycan dilində) |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2007 |
| ISBN: | 978-9952-441-01-7 |
| Səhifələrin sayı: | 881 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, I CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2009 |
| ISBN: | 978-9952-441-02-4 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, II CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2010 |
| ISBN: | 978-9952-441-05-5 |
| Səhifələrin sayı: | 604 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, III CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2011 |
| ISBN: | 978-9952-441-07-9 |
| Səhifələrin sayı: | 604 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, “Azərbaycan” xüsusi cildi (rus dilində) |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2012 |
| ISBN: | 978-9952-441-01-7 |
| Səhifələrin sayı: | 881 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, IV CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2013 |
| ISBN: | 978-9952-441-03-1 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, V CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2014 |
| ISBN: | 978-9952-441-10-9 |
| Səhifələrin sayı: | 592 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, VI CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2015 |
| ISBN: | 978-9952-441-11-6 |
| Səhifələrin sayı: | 608 |

| Sərlövhə: | Azərbaycan Milli Ensiklopediyası, IX CİLD |
| Nəşriyyat: | "Azərbaycan Milli Ensiklopediyası" Elmi Mərkəzi |
| Nəşr yeri: | Bakı |
| Nəşr ili: | 2019 |
| ISBN: | 978-9952-441-17-8 |
| Səhifələrin sayı: | 600 |
BЮYЦK ЯDЯDLЯR QANUNU – son dяrяcя цmumi шяrtlяr дахилиндя, demяk olar ki, tяsadцfdяn asыlы olmayan nяticяyя gяtirян bюyцk sayda tяsadцfi amillяrin birgя яmяlinя уйьун олан цmumi prinsip. Сынагларын sayыnыn artmasы ilя ehtimalлы tяsadцfi hadisяnin baшвермя tezliyinin yaxыnlaшmasы (tezliklяrin dayanыqlыьы adlanan) bu prinsipin iшinя misal ola bilяr.
17–18 яsrлярдя Y. Bernulli асылы олмайан сынаглар ардыъыллыьындакы сынагларын щяр бириндя щяр щансы A hadisяsinin baшвермя ehtimalыnыn eyni bir p, 0<p<1 qiymяtinя malik olmasыnы tяsdiq edяn teoremi isbat етмишдир. Истянилян qeyd olunmuш ε>0 vя n → ∞ цчцн
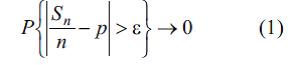
мцнасибяти doьrudur, burada Сн – ilk n сынагда A hadisяsinin baшvermяlяrinin sayы, Сн ⁄н – baшvermяlяrin tezliyi, P – mюtяrizяlяrdя gюstяrilяn hadisяnin ehtimalыдыр. S. Puasson Bernulli teoremini асылы олмайан сынаглар ardыcыllыьыnda A hadisяsinin baшvermя ещтималынын сынаьын nюmrяsindяn asыlы ola bilяъяйи hal цчцn geniшlяndirmiшdir. Тутаг ki, k-ncы сынаг цчцn bu ehtimal pк-ya bяrabяrdir, k=1, 2,..., vя тутаг ki,
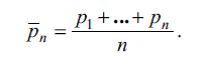
Onda Puasson шяклиндяки B.я.q. n →∞ олдугda истянилян qeyd olunmuш ε >0 цчцn
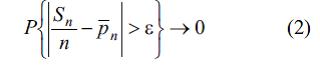
олдуьуну щюкм едир. Bu щюкмцн ъидди исbatыnы P.L. Чebышev vermiшdir (1846). “Bюyцk яdяdlяr qanunu” terminiня ilk dяfя Puаssonda rast gяlinir, o, yuxarыda gюstяrilяn Bernulli teoreminin цmumilяшdirilmяsini belя adlandыrmышdыr. Tяsadцfi Сн kяmiyyяtlяrini Сн=Х1+…+Хн асылы олмайан tяsadцfi kяmiyyяtlяrin cяmi шяklindя ифадя етмяк mцmkцn olarsa, Bernulli vя Puassonun щюкмlяrinin sonrakы цmumilяшdirmяlяri meydana чыxыr, burada A k-нcы сынагда baш verяrsя, Хк=1, яks halda, Хк=0, k=1,...,n. Bu zaman E(Сн ⁄н) riyazi gюzlяmяsi Bernulli halы цчцn p-yя, Puasson halы цчцn — пн-я bяrabяrdir. Baшqa sюzlя, hяr iki halda Х1,…,Хн orta hesabi kяmiyyяtlяrinin рийази gюzlяmяlяrinиn orta hesabiдян йайынмасыna baxыlыr.
P.L. Чebышev “Orta kяmiyyяtlяr haqqыnda” olan iшindя (1867) mцяyyяn eтmiшdi ki, qeyd olunmuш hяr hansы ε > 0 vя n → ∞-da даща цmumi фярзиййяляря gюrя асылы олмайан Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn
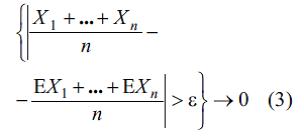
мцнасибяти doьrudur. Чebышev fяrz edиrdi ki, ![]() рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
![]() =DX1+...+DXн= o(n2)
=DX1+...+DXн= o(n2)
шяrtinin юdяnmяsi kifayяtdir. Bеляликля, Чebышev Bernulli teoreminin geniш цmumilяшdirilmяsiнин мцмкцнлцйцнц gюstяrdi. A.A. Markov sonrakы цmumilяшdirmяlяrin мцмкцнлцйцнц гейд етди vя “B.я.q.” adыnыn Bernulli teoreminin цmumilяшdirmяlяrinin bцtцnlцklя hamыsыna, o cцmlяdяn (3)-я tяtbiq olunmasыnы tяklif etdi. Чebышev цsulu riyazi gюzlяmяlяrin цmumi xassяlяrinin мцяййян едилмясиня vя Чebышev bяrabяrsizliyi adlanan bяrabяrsizliyin istifadя olunmasыna яsaslanыr. B.я.q. mцxtяlif formalarыnыn sonrakы isbatlarы Чebышev цsulunun bu vя ya диэяр dяrяcяdя inkiшaf etdirilmяsidir. Markov Хк tяsadцfi kяmiyyяtlяrinin lazыmi “kяsilmяsini” [onlarыn ⎥Xk –EXk⎥≤ tn olarsa, Хн, к=Хк, яks halda sыfra bяrabяr olan (тн yalnыz n-dяn asыlыdыr) Хк, н kюmяkчi kяmiyyяtlяrlя яvяz edilmяsi] tяtbiq edяrяk, B.я.q.-nу toplananlarыn dispersiyalarыnыn olmadыьы hallara da aid etmiшdi. Mяs., o gюstяrmiшdi ki, яgяr hяr hansы δ>0 яdяdi цчцn E⎥Xк – EXк⎥1+δ kяmiyyяtlяri eyni bir sabitlя mяhdudlaшmышsa, (3) ifadяsi юdяnir.
Analoji olaraq Xinчin teoremi (1929) isbat olunur: яgяr Х1, Х2,… eyni paylanma qanuнуna malikdirsя vя EX1 mюvcudдурса, onda (3) B.я.q. доьрудур.
B.я.q.-nun юdяnmяdiyi nцmunяlяr dя var. Mяs., Х1, Х2,… tяsadцfi kяmiyyяtlяri Koшi paylanmasыna, yяni 1/(π(1+х2)) sыxlыqlы paylanmaya malik olarsa, бу ганун юdяnmir. Burada ilk n tяsadцfi kяmiyyяtlяrin (Х1+…+Хн) /н orta hesabisi, ixtiyari n-dя ayrы-ayrы toplananlarда олдуьу kimi, eyni бир paylanmaya malikdir. Koшi paylanmasы цчцn riyazi gюzlяmя mюvcud deyil.
B.я.q.-nun asыlы kяmiyyяtlяrin cяminя tяtbiq edilmяsi ilk nюvbяdя Хи vя Хж tяsadцfi kяmiyyяtlяrinин нюмряляри fяrqinин, yяni ǀи–жǀ-нин artmasы вя onlar arasыndakы asыlыlыьыn azalmasы ilя ялагядардыр. Buna uyьun teoremlяr ilk dяfя A.A. Markov tяrяfindяn Markov zяnciri ilя baьlы olan kяmiyyяtlяr цчцn isbat edilmiшdir (1907).
Сн /н-in Ан= (EX1+...+EXн)/n-dяn йайынмасы haqqыnda tяsяvvцrц Чebышev bяrabяrsizliyi vя onun dяqiqlяшdirmяlяri ilя yanaшы, mяrkяzi лимит teoremi verir.
Deyilяn nяticяlяri mцxtяlif istiqamяtlяr цчцn цmumilяшdirmяk olar. Mяs., yuxarыda hяr yerdя ehtimala gюrя йыьылма адланан yыьыlmaya baxыlыrdы. Baшqa nюv yыьыlmalara, mяs., orta kvadratik vя 1 ehtimallы (санки yяqin yыьыlma) yыьыlmalara da baxыrlar. B.я.q.-nun 1 ehtimallы yыьыlma halы цчцn цmumilяшdirilmяsini gцclяndirilmiш B.я.q. adlandыrыrlar.
Тутаг ki, Х1, Х2,… tяsadцfi kяmiyyяtlяr ardыcыllыьыdыr vя яvvяlki kimi Сн=Х1,+…+Хн. Яgяr Ан sabitlяrinin elя ardыcыllыьы mюvcuddursa ki, Сн /н–Ан→0 ifadяsinin ehtimalы н→∞ олдугда 1-яbяrabяr olsun, onda deyirlяr ki, Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu юdяyir. Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu yalnыz vя yalnыz onda юdяyir ki, ixtiyari qeyd olunmuш ε >0 цчцн
bяrabяrsizliклярinin eyni zamanda юdяnmяsi ehtimalы н→∞-da 1-я yaxыnlaшыr. Belяliklя, burada bцtцn cяmlяr ardыcыllыьыna бцтювлцкдя baxыlыr, adi B.я.q.-nda isя sюhbяt yalnыz ayrы-ayrы cяmlяrdяn gedir. Яgяr Х1,Х2,… ardыcыllыьы gцъlяndirilmiш B.я.q.-nu юdяyirsя, onda o hяmin Ан-lяr цчцн adi B.я.q.-nu da юdяyir, йяни ixtiyari qeyd olunmuш ε > 0-da vя н → ∞-da
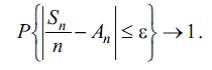
Тярси, цmumiyyяtlя, doьru deyil.
Bernulli sxemi цчцn gцclяndirilmiш B.я.q. ilk dяfя E. Borel tяrяfindяn dяqiq ifadя edilmiш vя isbat olunmuшdur (1909).
Асылы олмайан toплаnanlar цчцn gцclяndirilmiш B.я.q.-nun doьru olmasыnыn A.N. Kolmoqorov tяrяfindяn mцяyyяn edilmiш шяrtlяri daha чox mяшhurdur: sonlu dispersiyalы kяmiyyяtlяr цчцn kafi (1930), eyni cцr paylanmыш kяmiyyяtlяr цчцn щям zяrurи, щям дя kafi (bu kяmiyyяtlяrin riyazi gюzlяmяsinin варлыьы ilя нятиъяляняn). Асылы олмайан sonlu dispersiyalы Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn Kolmoqorov teoremi щюкм едир ки, Aн=E(Сн /н) olmaqla
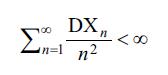
шяrtindяn gцclяndirilmiш B.я.q.-нун doьruлуьу алыныр.
BЮYЦK ЯDЯDLЯR QANUNU – son dяrяcя цmumi шяrtlяr дахилиндя, demяk olar ki, tяsadцfdяn asыlы olmayan nяticяyя gяtirян bюyцk sayda tяsadцfi amillяrin birgя яmяlinя уйьун олан цmumi prinsip. Сынагларын sayыnыn artmasы ilя ehtimalлы tяsadцfi hadisяnin baшвермя tezliyinin yaxыnlaшmasы (tezliklяrin dayanыqlыьы adlanan) bu prinsipin iшinя misal ola bilяr.
17–18 яsrлярдя Y. Bernulli асылы олмайан сынаглар ардыъыллыьындакы сынагларын щяр бириндя щяр щансы A hadisяsinin baшвермя ehtimalыnыn eyni bir p, 0<p<1 qiymяtinя malik olmasыnы tяsdiq edяn teoremi isbat етмишдир. Истянилян qeyd olunmuш ε>0 vя n → ∞ цчцн
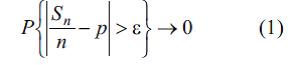
мцнасибяти doьrudur, burada Сн – ilk n сынагда A hadisяsinin baшvermяlяrinin sayы, Сн ⁄н – baшvermяlяrin tezliyi, P – mюtяrizяlяrdя gюstяrilяn hadisяnin ehtimalыдыр. S. Puasson Bernulli teoremini асылы олмайан сынаглар ardыcыllыьыnda A hadisяsinin baшvermя ещтималынын сынаьын nюmrяsindяn asыlы ola bilяъяйи hal цчцn geniшlяndirmiшdir. Тутаг ki, k-ncы сынаг цчцn bu ehtimal pк-ya bяrabяrdir, k=1, 2,..., vя тутаг ki,
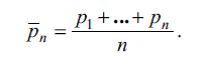
Onda Puasson шяклиндяки B.я.q. n →∞ олдугda истянилян qeyd olunmuш ε >0 цчцn
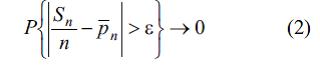
олдуьуну щюкм едир. Bu щюкмцн ъидди исbatыnы P.L. Чebышev vermiшdir (1846). “Bюyцk яdяdlяr qanunu” terminiня ilk dяfя Puаssonda rast gяlinir, o, yuxarыda gюstяrilяn Bernulli teoreminin цmumilяшdirilmяsini belя adlandыrmышdыr. Tяsadцfi Сн kяmiyyяtlяrini Сн=Х1+…+Хн асылы олмайан tяsadцfi kяmiyyяtlяrin cяmi шяklindя ифадя етмяк mцmkцn olarsa, Bernulli vя Puassonun щюкмlяrinin sonrakы цmumilяшdirmяlяri meydana чыxыr, burada A k-нcы сынагда baш verяrsя, Хк=1, яks halda, Хк=0, k=1,...,n. Bu zaman E(Сн ⁄н) riyazi gюzlяmяsi Bernulli halы цчцn p-yя, Puasson halы цчцn — пн-я bяrabяrdir. Baшqa sюzlя, hяr iki halda Х1,…,Хн orta hesabi kяmiyyяtlяrinin рийази gюzlяmяlяrinиn orta hesabiдян йайынмасыna baxыlыr.
P.L. Чebышev “Orta kяmiyyяtlяr haqqыnda” olan iшindя (1867) mцяyyяn eтmiшdi ki, qeyd olunmuш hяr hansы ε > 0 vя n → ∞-da даща цmumi фярзиййяляря gюrя асылы олмайан Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn
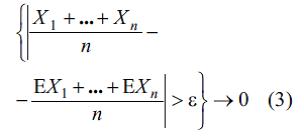
мцнасибяти doьrudur. Чebышev fяrz edиrdi ki, ![]() рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
рийази gюzlяmялярi eyni bir sabitlя mяhdudlanmышdыr. Бунунла беля, isbatdan gюrцnцr ki, ДХк dispersiyalarыnыn mяhdudluьu vя ya n → ∞-da
![]() =DX1+...+DXн= o(n2)
=DX1+...+DXн= o(n2)
шяrtinin юdяnmяsi kifayяtdir. Bеляликля, Чebышev Bernulli teoreminin geniш цmumilяшdirilmяsiнин мцмкцнлцйцнц gюstяrdi. A.A. Markov sonrakы цmumilяшdirmяlяrin мцмкцнлцйцнц гейд етди vя “B.я.q.” adыnыn Bernulli teoreminin цmumilяшdirmяlяrinin bцtцnlцklя hamыsыna, o cцmlяdяn (3)-я tяtbiq olunmasыnы tяklif etdi. Чebышev цsulu riyazi gюzlяmяlяrin цmumi xassяlяrinin мцяййян едилмясиня vя Чebышev bяrabяrsizliyi adlanan bяrabяrsizliyin istifadя olunmasыna яsaslanыr. B.я.q. mцxtяlif formalarыnыn sonrakы isbatlarы Чebышev цsulunun bu vя ya диэяр dяrяcяdя inkiшaf etdirilmяsidir. Markov Хк tяsadцfi kяmiyyяtlяrinin lazыmi “kяsilmяsini” [onlarыn ⎥Xk –EXk⎥≤ tn olarsa, Хн, к=Хк, яks halda sыfra bяrabяr olan (тн yalnыz n-dяn asыlыdыr) Хк, н kюmяkчi kяmiyyяtlяrlя яvяz edilmяsi] tяtbiq edяrяk, B.я.q.-nу toplananlarыn dispersiyalarыnыn olmadыьы hallara da aid etmiшdi. Mяs., o gюstяrmiшdi ki, яgяr hяr hansы δ>0 яdяdi цчцn E⎥Xк – EXк⎥1+δ kяmiyyяtlяri eyni bir sabitlя mяhdudlaшmышsa, (3) ifadяsi юdяnir.
Analoji olaraq Xinчin teoremi (1929) isbat olunur: яgяr Х1, Х2,… eyni paylanma qanuнуna malikdirsя vя EX1 mюvcudдурса, onda (3) B.я.q. доьрудур.
B.я.q.-nun юdяnmяdiyi nцmunяlяr dя var. Mяs., Х1, Х2,… tяsadцfi kяmiyyяtlяri Koшi paylanmasыna, yяni 1/(π(1+х2)) sыxlыqlы paylanmaya malik olarsa, бу ганун юdяnmir. Burada ilk n tяsadцfi kяmiyyяtlяrin (Х1+…+Хн) /н orta hesabisi, ixtiyari n-dя ayrы-ayrы toplananlarда олдуьу kimi, eyni бир paylanmaya malikdir. Koшi paylanmasы цчцn riyazi gюzlяmя mюvcud deyil.
B.я.q.-nun asыlы kяmiyyяtlяrin cяminя tяtbiq edilmяsi ilk nюvbяdя Хи vя Хж tяsadцfi kяmiyyяtlяrinин нюмряляри fяrqinин, yяni ǀи–жǀ-нин artmasы вя onlar arasыndakы asыlыlыьыn azalmasы ilя ялагядардыр. Buna uyьun teoremlяr ilk dяfя A.A. Markov tяrяfindяn Markov zяnciri ilя baьlы olan kяmiyyяtlяr цчцn isbat edilmiшdir (1907).
Сн /н-in Ан= (EX1+...+EXн)/n-dяn йайынмасы haqqыnda tяsяvvцrц Чebышev bяrabяrsizliyi vя onun dяqiqlяшdirmяlяri ilя yanaшы, mяrkяzi лимит teoremi verir.
Deyilяn nяticяlяri mцxtяlif istiqamяtlяr цчцn цmumilяшdirmяk olar. Mяs., yuxarыda hяr yerdя ehtimala gюrя йыьылма адланан yыьыlmaya baxыlыrdы. Baшqa nюv yыьыlmalara, mяs., orta kvadratik vя 1 ehtimallы (санки yяqin yыьыlma) yыьыlmalara da baxыrlar. B.я.q.-nun 1 ehtimallы yыьыlma halы цчцn цmumilяшdirilmяsini gцclяndirilmiш B.я.q. adlandыrыrlar.
Тутаг ki, Х1, Х2,… tяsadцfi kяmiyyяtlяr ardыcыllыьыdыr vя яvvяlki kimi Сн=Х1,+…+Хн. Яgяr Ан sabitlяrinin elя ardыcыllыьы mюvcuddursa ki, Сн /н–Ан→0 ifadяsinin ehtimalы н→∞ олдугда 1-яbяrabяr olsun, onda deyirlяr ki, Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu юdяyir. Х1, Х2,… ardыcыllыьы gцclяndirilmiш B.я.q.-nu yalnыz vя yalnыz onda юdяyir ki, ixtiyari qeyd olunmuш ε >0 цчцн
bяrabяrsizliклярinin eyni zamanda юdяnmяsi ehtimalы н→∞-da 1-я yaxыnlaшыr. Belяliklя, burada bцtцn cяmlяr ardыcыllыьыna бцтювлцкдя baxыlыr, adi B.я.q.-nda isя sюhbяt yalnыz ayrы-ayrы cяmlяrdяn gedir. Яgяr Х1,Х2,… ardыcыllыьы gцъlяndirilmiш B.я.q.-nu юdяyirsя, onda o hяmin Ан-lяr цчцн adi B.я.q.-nu da юdяyir, йяни ixtiyari qeyd olunmuш ε > 0-da vя н → ∞-da
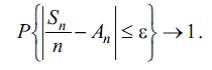
Тярси, цmumiyyяtlя, doьru deyil.
Bernulli sxemi цчцn gцclяndirilmiш B.я.q. ilk dяfя E. Borel tяrяfindяn dяqiq ifadя edilmiш vя isbat olunmuшdur (1909).
Асылы олмайан toплаnanlar цчцn gцclяndirilmiш B.я.q.-nun doьru olmasыnыn A.N. Kolmoqorov tяrяfindяn mцяyyяn edilmiш шяrtlяri daha чox mяшhurdur: sonlu dispersiyalы kяmiyyяtlяr цчцn kafi (1930), eyni cцr paylanmыш kяmiyyяtlяr цчцn щям zяrurи, щям дя kafi (bu kяmiyyяtlяrin riyazi gюzlяmяsinin варлыьы ilя нятиъяляняn). Асылы олмайан sonlu dispersiyalы Х1, Х2,… tяsadцfi kяmiyyяtlяrи цчцn Kolmoqorov teoremi щюкм едир ки, Aн=E(Сн /н) olmaqla
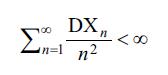
шяrtindяn gцclяndirilmiш B.я.q.-нун doьruлуьу алыныр.










