АВТОМОРФ ФУНКСИЙА (авто… +йун. µορφή – эюрцнцш) – аргументи мцяййян кясри-хятти чевирмяляря мяруз галдыгда гиймятляри дяйишмяйян мераморф функсийа. Периодик, о ъцмлядян еллиптик функсийалар А.ф-йа аиддир.

Мяс., яэяр эюстярилян чевирмяляр тамдырса вя з'=з+ω шяклиндядирся (ω – сыфырдан фяргли комплекс ядяд), онда ф(з+ω)=ф(з) бярабярлийини юдяйян  А.ф.лар (йяни ω периодлу функсийалар) алыныр. Бу мисалда функсийанын гиймятини дяйишмяйян  чевирмя,  мцстявинин  ω  вектору гядяр  йердяйишмясидир.  Бу  йердяйишмя ня гядяр тякрар олунса да, функсийаны дяйишдирмир. Нятиъядя ф(з) функсийасыны дяйишмяйян  з'=з+нω  (н=0,  ±1,  ±2,…) хятти чевирмяляр групу алыныр.

Цмуми щалда, тутаг ки, Г – мцяййян кясри-хятти чевирмяляр групудур:

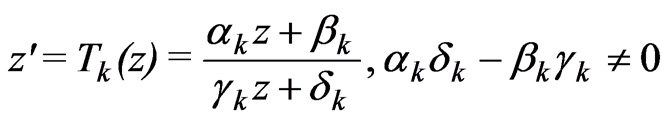
 вя Д еля областдыр ки, бу чевирмялярин щяр бири  иля  юз-юзцня  иникас  олунур.  Онда ф [Тк(з)]=ф(з),  к  =  1, 2,  …  олдугда,  Д областында биргиймятли вя аналитик олан ф функсийасы А.ф.-дыр (верилян Г групуна эюря). Ян мцщцм щал Д областынын даиря вя йа йарыммцстяви олмасыдыр. Беля областа Лобачевски мцстявисинин тясвири кими (бах Лобачевски щяндясяси), Г чевирмяляр  групуна  ися  Лобачевски  мцстявисиндя щярякят кими бахмаг олар. Уйьун А.ф.-лара Евклид мцстявисиндяки йердяйишмялярин Лобачевски мцстявисиндяки щярякятляр иля явяз олундуьу периодик функсийаларын цмумиляшмяси кими бахмаг олар. А.ф.-нын цмуми нязяриййясинин йаранмасында  А.  Пуанкаре  вя  Ф.  Клейнин ишляри мцщцм рол ойнамышдыр.