БÁЗИС, р и й а з и й й а т д а – бахылан чохлуьун вя йа фязанын бцтцн елементля рини ифадя етмяк (тясвир етмяк) цчцн минимал елементляр йыьыны. Б. анлайышы ъябрдя, функсионал анализдя, щяндясядя, тополоэийада, рийази мянтигдя истифадя едилир. Б. анлайышынын рийазиййатын щансы бюлмясиндя истифадя едилмясиндян асылы олараг, “минимал”, “ифадя етмяк” (“тясвир етмяк”) сюзляри конкрет мязмун дашыйыр. Координатлары х₁, …, х_н олан векторлардан ibarяt сонлу юлчцлц щягиги (комплекс) Р^н (Ъ^н) вектор фязасында {е₁,…, е_н} векторлар йыьыны Б.-ин ян йахшы нцмунясидир; бурада е_к – к-ъы координаты 1-я, галанлары ися сыфра бярабяр олан вектордур, к = 1,…, н. Р^н (Ъ^н) фязасынын щяр щансы елементини {е₁, …, е_н} елементляринин хятти комбинасийасы кими, йяни ядядя вурулмуш бу елементлярин ъями кими ифадя етмяк олар. Бурада минималlыq {е₁,…, е_н} йыьынынын щеч бир щиссясинин бу хассяйя малик олмадыьыны эюстярир.

Сонлу Б.-и олмайан вектор фязасы сонсуз юлчцлц адландырылыр. Сонсуз юлчцлц сепарабел Банах фязасында Б.-и ашаьыдакы хассяйя малик {е_1, е_2,…} елементляринин щесаби йыьыны кими тяйин олунур: фязанын щяр щансы х елементини йеэаня olaraq

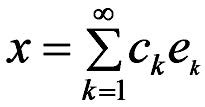
сырасы шяклиндя тясвир едилир; бурада ъ_к, к=1, 2,… – ядядлярдир, сыра ися фяза нормасы цzrя йыьылыр. Ихтийари сепарабел Банах фязасында Б.-in мювъудлуьуна даир Банахыn мялум проблеми Исвеч рийазиййатчысы П. Енфло тяряфиндян мянфи щялл едилмишди (1974). Банах фязасында мцхтялиф нюв Б. тяйин етмяк олар – онларын юйрянилмяси эениш бир нязяриййянин мювзусудур. Сепарабел Щилберт фязаларында ян чох ортонормалашдырылмыш Б.-ляр, йяни скалйар щасилляри (е_и, е_ж)=0, и ≠ ж вя (е_и, е_и)=1, и=1,2,… олан е₁, е_2,… Б.-ляр тятбиг едилир. Лебег цzrя п-ъи дяряъядян интегралланан функсийалардан тяшкил олунмуш Лп [0,1], п>1 фязаларында  тригонометрик системи Б.-я ян мцщцм мисалдыр. Бу систем Л₂ [0,1]-дя ортонормалашдырылмыш Б.-дир, Л₁ [0,1]-дя ися Б. дейилдир.