биринъи нюв силиндрик функсийалар; даиряви вя силиндрик симметрийалы областларда бахылан физики просеслярин (истиликкечирмя, диффузийа, рягсляр вя с.) юйрянилмясиндя истифадя олунур. Б.ф. Бессел тянлийинин щяллидир. п (– ∞<п<∞) тяртибли (индексли) Жп Б.ф. бцтцн x-ляря эюря йыьылан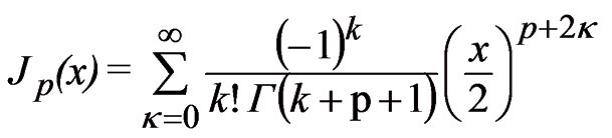 



сырасы иля ифадя олунур; бурада Г– гамма функсийасыдыр. x >0 олдугда Жп(х)-ин графики сюнян рягслярин яйрисини ифадя едир. Жп(х)-ин сонсуз сайда сыфырлары вардыр; сыранын биринъи топлананлары |х|-ин кичик гиймятляриндя Жп(х)-ин асимптотуну верир, х>0 гиймятляриндя

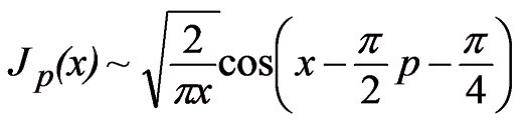
асимптотик тясвири доьрудур. 

   тяртибли Б.ф. (бурада н – там ядяддир), елементар функсийалар васитясиля ифадя олунур; хцсуси щалда, 



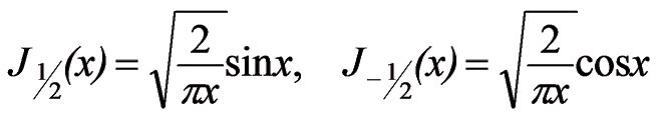
 Б.ф. (бурада Жп(х)=0, тянлийинин мцсбят кюкляри, л – щансыса мцсбят ядяддир) (0, л) интервалында х чякили ортогонал систем ямяля эятирир. 
Ж₀ функсийасы илк дяфя Д. Бернулли тяряфиндян 1732 илдя аьыр зянъирлярин рягсляриня щяср олунмуш ишиндя арашдырылмышдыр; Л. Ейлер 1738 илдя даиряви мембранын рягсиня даир мясяляйя бахараг п=н там гиймятляря малик Бессел тянлийиня эялмиш вя х-ин дяряъяляриня эюря сыра шяклиндя Жн(х)-ин ифадясини тапмышдыр; сонралар о бу ифадяни п-нин ихтийари гиймятляри цчцн эенишляндирмишдир. Ф. Бессел 1824 илдя планетлярин Эцняш ятрафында щярякятинин юйрянилмяси иля ялагядар Ж_п(х) функсийасыны арашдырмыш вя Ж₀(х), Ж₁(х) цчцн илк ъядвялляри тяртиб етмишдир.