БЯРАБЯРСИЗЛИК – < (кичик), ≤ (кичик вя йа бярабяр), > (бюйцк), ≥ (бюйцк вя йа бярабяр), ≠ (бярабяр дейил) ишаряляриндян биринин васитясиля а1 вя а2 ядядлярини ялагяляндирян мцнасибят, йяни
а1< а2 , а1 ≤ а2 , а1> а2 ,
а1 ≥ а2 , а1 ≠ а2.
Бязян бир нечя Б. бирликдя йазылыр, мяс.,
а < б < ъ
Б.-ин бярабярликлярля бир чох цмуми хцсусиййятляри вардыр. Мяс., Б.-ин щяр ики тяряфиня ейни бир ядяди ялавя етсяк (вя йа чыхсаг), о дяйишмяз. Еляъя дя Б.-ин щяр ики тяряфини ейни бир мцсбят ядядя вурмаг олар. Лакин Б.-ин щяр ики тяряфини мянфи ядядя вурсаг, Б.-ин мянасы яксиня дяйишяр (йяни > ишаряси < ишаряси иля, < ишаряси ися> ишаряси иля явяз олунар). А < Б вя Ъ < Д бярабярсизликляриндян А + Ъ < Б + Д вя А – Д < Б – Ъ алыныр, йяни ейни адлы (А < Б вя Ъ< Д) Б.-ляри щядбящяд топламаг, мцхтялиф адлы (А < Б вя Д > Ъ) Б.-ляри ися щядбящяд чыхмаг олар. Яэяр А, Б, Ъ вя Д ядядляри мцсбятдирся, онда А < Б вя Ъ < Д бярабярсизликляриндян щям дя АЪ < БД вя А/Д < Б/Ъ алыныр, йяни ейни адлы Б.-ляри (мцсбят ядядляр арасында) щядбящяд вурмаг, мцхтялиф адлылары ися щядбящяд бюлмяк олар.
Мцхтялиф ядяди гиймятляр алан кямиййятлярин дахил олдуьу Б. бу кямиййятлярин бязи гиймятляри цчцн доьру, диэяр гиймятляри цчцн доьру олмайа биляр. Мяс., х2 – 4х + 3 > 0 бярабярсизлийи х = 4 гиймяти цчцн доьру вя х = 2 гиймяти цчцн доьру дейил. Бу тип Б.-ляр цчцн онларын щялли мясяляси, йяни Б.-йя дахил олан кямиййятлярин сярщядляринин Б.-ин доьру олмасыны тямин едян гиймятляринин тапылмасы мясяляси ортайа чыхыр. Беляликля, х2– 4х + 3 > 0 бярабярсизлийини (х–1)(х–3) > 0 шяклиндя йазанда анлашылыр ки, о, х<1, х>3 бярабярсизликляриндян бирини юдяйян бцтцн х-ляр цчцн доьрудур вя онлар щямин Б.-ин щяллидир.
Ашаьыда Б.-йя дахил олан дяйишянлярин бу вя йа диэяр дяйишмя областында ейнилик кими юдянилян бязи Б.-ляр эюстярилмишдир.
1) М о д у л л а р ц ч ц н б я р а б я р с и з л и к. Истянилян щягиги вя йа комплекс а1, а2, …, ан ядядляри цчцн
| а1+а2+…+ан| ≤ | а1| + | а2| +…+| ан |
Б.-и доьрудур.
2) Щармоник, щяндяси, ядяди вя квадратик орталары ялагяляндирян цчцн Б. даща чох мялумдур:
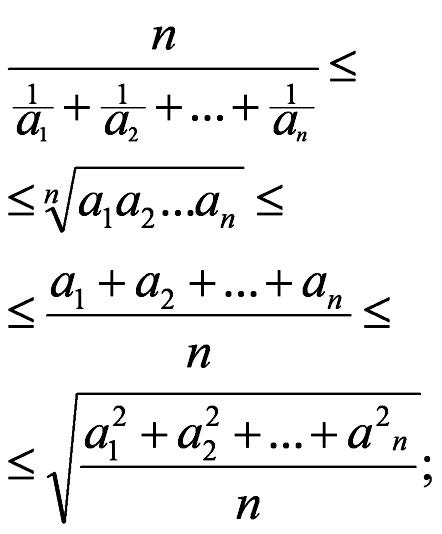
бурада а1, а2, …., ан мцсбят ядядлярдир.
3) Ъ я м л я р ц ч ц н б я р а б я р с и з л и к л я р в я о н л а р ы н и н т е г р а л а н а л о г л а р ы. Мяс., Бунйаковски бярабярсизлийи, Щюлдер бярабярсизлийи, Коши бярабярсизлийи беляляриндяндир.
4) Г ц в в я т л я р в я я д я д л я р ц ч ц н б я р а б я р с и з л и к л я р. Бурада ян чох мялум олан Минковски бярабясизлийи вя онун сыралар вя интеграллар щаллары цчцн цмумиляшмясидир.
5) Б я з и а р д ы ъ ы л л ы г л а р в я ф у н к с и й а л а р с и н и ф л я р и ц ч ц н б я р а б я р с и з л и к л я р. Монотон ардыъыллыглар цчцн Чебышев бярабярсизлийи вя габарыг функсийалар цчцн Иенсен бярабярсизлийи мисал ола биляр.
6) Х я т т и б я р а б я р с и з л и к л я р.
аи1х1 + аи 2х2 +…+ аи нхн ≥ би , и =1, 2, … , н
шяклиндя Б. системиня бахылыр. Бу Б. системинин щялляр топлусу н-юлчцлц (х1 , х2 , …, хн) фязасында щяр щансы габарыг чохцзлцнц тясвир едир; хятти бярабярсизликляр нязяриййясинин мясяляси бу чохцзлцнцн хассялярини юйрянмякдян ибарятдир.
Б. рийазиййатын бцтцн сащяляри цчцн ящямиййятлидир. Ядядляр нязяриййясиндя бу фяннин там бир фясли – Диофант йахынлашмалары – бцтювлцкля Б.-я ясасланыр; ядядлярин аналитик нязяриййяси дя тез-тез бярабярсизликлярля ямялиййат апарыр. Щяндясядя габарыг ъисмляр нязяриййясиндя вя изопериметрик мясялядя Б.-я щямишя раст эялинир. Ещтимал нязяриййясиндя бир чох ганунлар Б.-ин кюмяйи иля ифадя олунур. Диференсиал тянликляр нязяриййясиндя диференсиал бярабярсизликлярдян истифадя едилир. Функсийалар нязяриййясиндя чохщядлилярин вя тригонометрик полиномларын тюрямяляри цчцн ардыъыл олараг мцхтялиф Б.-ляр истифадя олунур. Функсионал анализдя функсионал фязада норманын тяйини заманы тяляб олунур ки, о, ║x+y║ ≤ ║x║+ ║y║ цчбуъаг Б.-ини юдясин. Бир чох классик Б.-ляр мащиййятъя хятти функсионалын вя йа хятти операторун нормасынын гиймятини бу вя йа диэяр фязада тяйин едир вя йа онлары гиймятляндирир (бах Бессел бярабярсизлийи). Щесаблама рийазиййатында Б. мясялянин тягриби щяллинин хятасынын гиймятляндирилмясиндя тятбиг едилир.














